题目内容
12.焦点为(0,±3),且与双曲线$\frac{x^2}{2}-{y^2}=1$有相同的渐近线的双曲线方程是( )| A. | $\frac{x^2}{3}-\frac{y^2}{6}=1$ | B. | $\frac{y^2}{3}-\frac{x^2}{6}=1$ | C. | $\frac{y^2}{6}-\frac{x^2}{3}=1$ | D. | $\frac{x^2}{6}-\frac{y^2}{3}=1$ |
分析 根据:“与双曲线$\frac{x^2}{2}-{y^2}=1$有相同的渐近线”设所求的双曲线方程是$\frac{{x}^{2}}{2}-{y}^{2}$=k,由焦点(0,±3)在y轴上,知k<0,故双曲线方程是$\frac{{y}^{2}}{-k}-\frac{{x}^{2}}{-2k}=1$,据c2=9,求出k值,即得所求的双曲线方程.
解答 解:由题意知,可设所求的双曲线方程是$\frac{{x}^{2}}{2}-{y}^{2}$=k,
∵焦点(0,±3)在y轴上,∴k<0,
所求的双曲线方程是$\frac{{y}^{2}}{-k}-\frac{{x}^{2}}{-2k}=1$,
由-2k-k=c2=9,∴k=-3,
故所求的双曲线方程是$\frac{{y}^{2}}{3}-\frac{{x}^{2}}{6}=1$,
故选:B.
点评 本题考查双曲线的标准方程,以及双曲线的简单性质的应用,解题的关键是根据渐近线方程相同设所求的双曲线方程是$\frac{{x}^{2}}{2}-{y}^{2}$=k,属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
20.将函数f(x)=sin2x的图象向左平移$\frac{π}{4}$个长度单位,得到函数g(x)的图象,则g(x)的单调递增区间是( )
| A. | (kπ-$\frac{π}{2}$,kπ)(k∈Z) | B. | (kπ,kπ+$\frac{π}{2}$)(k∈Z) | C. | (kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$)(k∈Z) | D. | (kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$)(k∈Z) |
7.“a=2”是直线“ax-2y=0与直线x-y+1=0平行的”( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
17. 图为某个几何体的三视图,则该几何体的表面积为( )
图为某个几何体的三视图,则该几何体的表面积为( )
 图为某个几何体的三视图,则该几何体的表面积为( )
图为某个几何体的三视图,则该几何体的表面积为( )| A. | 32 | B. | 16+16$\sqrt{2}$ | C. | 48 | D. | 16+32$\sqrt{2}$ |
4.设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(3)=0,当x<0时,xf′(x)+f(x)>0,则有( )
| A. | f(-3)<f(1)<f(2) | B. | f(2)<f(-3)<f(1) | C. | f(1)<f(-3)<f(2) | D. | f(-3)<f(2)<f(1) |
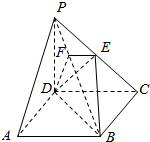 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.