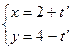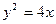题目内容
设椭圆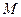 :
: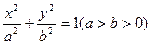 的离心率为
的离心率为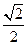 ,点
,点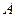 (
(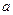 ,0),
,0),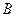 (0,
(0,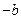 ),原点
),原点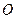 到直线
到直线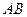 的距离为
的距离为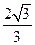 .
.
(Ⅰ)求椭圆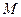 的方程;
的方程;
(Ⅱ)设点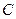 为(
为(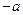 ,0),点
,0),点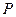 在椭圆
在椭圆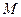 上(与
上(与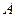 、
、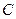 均不重合),点
均不重合),点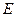 在直线
在直线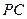 上,若直线
上,若直线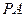 的方程为
的方程为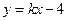 ,且
,且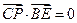 ,试求直线
,试求直线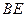 的方程.
的方程.
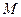 :
: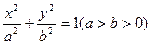 的离心率为
的离心率为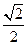 ,点
,点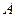 (
(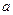 ,0),
,0),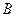 (0,
(0,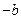 ),原点
),原点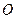 到直线
到直线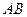 的距离为
的距离为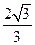 .
.(Ⅰ)求椭圆
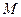 的方程;
的方程;(Ⅱ)设点
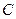 为(
为(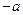 ,0),点
,0),点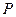 在椭圆
在椭圆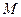 上(与
上(与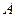 、
、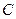 均不重合),点
均不重合),点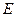 在直线
在直线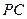 上,若直线
上,若直线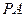 的方程为
的方程为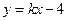 ,且
,且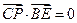 ,试求直线
,试求直线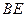 的方程.
的方程.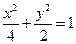 ,直线
,直线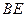 的方程为
的方程为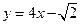
解 (Ⅰ)由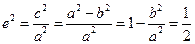 得
得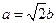
由点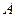 (
(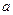 ,0),
,0),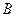 (0,
(0,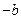 )知直线
)知直线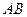 的方程为
的方程为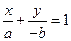 ,
,
于是可得直线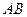 的方程为
的方程为
因此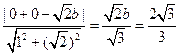 ,得
,得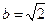 ,
,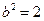 ,
,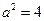 ,
,
所以椭圆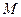 的方程为
的方程为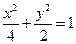
(Ⅱ)由(Ⅰ)知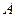 、
、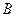 的坐标依次为(2,0)、
的坐标依次为(2,0)、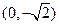 ,
,
因为直线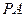 经过点
经过点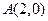 ,所以
,所以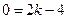 ,得
,得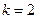 ,
,
即得直线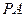 的方程为
的方程为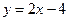
因为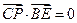 ,所以
,所以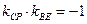 ,即
,即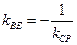
设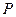 的坐标为
的坐标为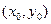 ,则
,则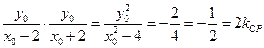
得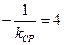 ,即直线
,即直线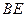 的斜率为4
的斜率为4
又点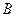 的坐标为
的坐标为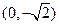 ,因此直线
,因此直线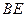 的方程为
的方程为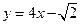
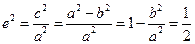 得
得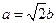
由点
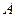 (
(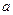 ,0),
,0),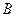 (0,
(0,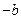 )知直线
)知直线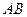 的方程为
的方程为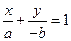 ,
,于是可得直线
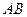 的方程为
的方程为
因此
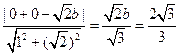 ,得
,得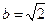 ,
,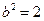 ,
,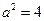 ,
,所以椭圆
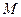 的方程为
的方程为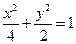
(Ⅱ)由(Ⅰ)知
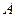 、
、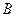 的坐标依次为(2,0)、
的坐标依次为(2,0)、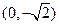 ,
,因为直线
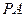 经过点
经过点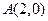 ,所以
,所以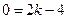 ,得
,得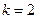 ,
,即得直线
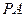 的方程为
的方程为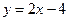
因为
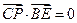 ,所以
,所以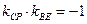 ,即
,即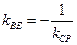
设
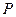 的坐标为
的坐标为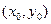 ,则
,则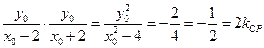
得
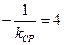 ,即直线
,即直线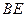 的斜率为4
的斜率为4 又点
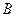 的坐标为
的坐标为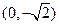 ,因此直线
,因此直线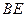 的方程为
的方程为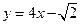

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
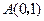 ,点
,点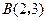 ,曲线
,曲线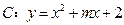 ,若曲线与线段
,若曲线与线段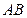 有两个不同的交点,求实数
有两个不同的交点,求实数 的范围.
的范围. 点M在y轴上,且
点M在y轴上,且 ,点C在x轴上移动,(I)求点B的轨迹E的方程;(II)过点
,点C在x轴上移动,(I)求点B的轨迹E的方程;(II)过点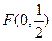 的直线l与曲线E交于P、Q两点,
的直线l与曲线E交于P、Q两点,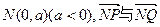 的夹角为
的夹角为
 为
为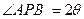 ,且
,且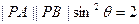 . (I)求动点P的轨迹G的方程;(II)过点B的直线
. (I)求动点P的轨迹G的方程;(II)过点B的直线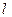 与轨迹G交于两点M,N.试问在x轴上是否存在定点C ,使得
与轨迹G交于两点M,N.试问在x轴上是否存在定点C ,使得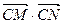 为常数.若存在,求出点C的坐标;若不存在,说明理由.
为常数.若存在,求出点C的坐标;若不存在,说明理由.

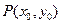 在椭圆
在椭圆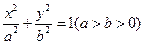 上,
上,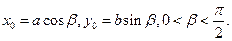 直线
直线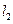 与直线
与直线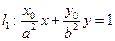 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为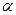 ,直线
,直线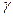 .
.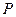 是椭圆
是椭圆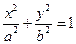 与直线
与直线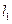 的唯一交点;
的唯一交点; 
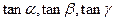 构成等比数列.
构成等比数列.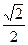
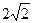
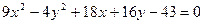
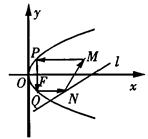
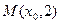 发出的光线沿平行于抛物线
发出的光线沿平行于抛物线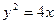 的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线
的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线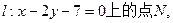 再反射后又射回点M,则 x0= .
再反射后又射回点M,则 x0= .