题目内容
已知椭圆 以双曲线
以双曲线 的焦点为顶点,以双曲线的顶点为焦点。
的焦点为顶点,以双曲线的顶点为焦点。
(1)求椭圆 的方程;
的方程;
(2)若直线 与椭圆
与椭圆 相交于点
相交于点 ,
, 两点(
两点( ,
, 不是左右顶点),且以线段
不是左右顶点),且以线段 为直径的圆过椭圆
为直径的圆过椭圆 左顶点
左顶点 ,求证:直线
,求证:直线 过定点,并求出该定点的坐标。
过定点,并求出该定点的坐标。
解:(1) ;
;
(2)设 ,联立方程组
,联立方程组 ,得
,得 。
。
又因为以 为直径的圆过点
为直径的圆过点 ,所以
,所以 ,即
,即 ,整理得
,整理得
 ,所以
,所以 或
或 且满足
且满足 ,若
,若 ,则直线
,则直线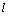 恒过定点
恒过定点 ,不合题意;若
,不合题意;若 ,则直线
,则直线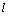 恒过定点
恒过定点 。
。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
 ,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是______________。
,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是______________。
 在圆C:
在圆C: 上运动,则动点
上运动,则动点 的轨迹方程是_______________
的轨迹方程是_______________ 中,
中, ,
, ,
, ,则
,则 ,则它所表示的曲线的焦点坐标为 ( )
,则它所表示的曲线的焦点坐标为 ( ) (B)
(B) (C)
(C) (D)
(D)
 相等的是( )
相等的是( ) B.
B.
 D.
D.
 (
( 是虚数单位)是纯虚数,则实数
是虚数单位)是纯虚数,则实数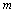 的值为 .
的值为 . B.8+
B.8+ C.8+
C.8+ D.8+
D.8+
