题目内容
已知向量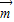
=（sinx，1），
=（
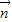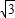Acosx，
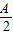cos2x）（A＞0），函数f（x）=
•
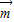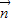的最大值为6．（Ⅰ）求A；
（Ⅱ）将函数y=f（x）的图象像左平移
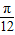个单位，再将所得图象各点的横坐标缩短为原来的
倍，纵坐标不变，得到函数y=g（x）的图象．求g（x）在[0，
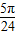]上的值域．
【答案】分析：（Ⅰ）利用向量的数量积展开，通过二倍角公式以及两角和的正弦函数化为，一个角的一个三角函数的形式，通过最大值求A；
（Ⅱ）通过将函数y=f（x）的图象像左平移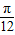
个单位，再将所得图象各点的横坐标缩短为原来的
倍，纵坐标不变，得到函数y=g（x）的图象．求出g（x）的表达式，通过x∈[0，
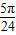]求出函数的值域．
解答：解：（Ⅰ）函数f（x）=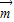
•
=
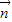
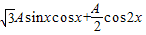
=A（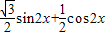
）
=Asin（2x+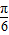
）．
因为A＞0，由题意可知A=6．
（Ⅱ）由（Ⅰ）f（x）=6sin（2x+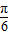
）．
将函数y=f（x）d的图象向左平移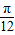
个单位后得到，
y=6sin[2（x+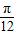
）+
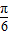]=6sin（2x+
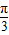）．的图象．再将所得图象各点的横坐标缩短为原来的
倍，
纵坐标不变，得到函数y=6sin（4x+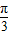
）的图象．因此g（x）=6sin（4x+
）．
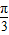因为x∈[0，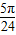
]，所以4x+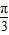
，
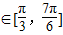故g（x）在[0，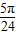
]上的值域为[-3，6]．
点评：本题考查三角函数的最值，平面向量数量积的坐标表示、模、夹角，正弦函数的定义域和值域，函数y=Asin（ωx+φ）的图象变换，考查计算能力．
（Ⅱ）通过将函数y=f（x）的图象像左平移
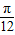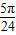个单位，再将所得图象各点的横坐标缩短为原来的倍，纵坐标不变，得到函数y=g（x）的图象．求出g（x）的表达式，通过x∈[0，]求出函数的值域．解答：解：（Ⅰ）函数f（x）=
•=
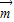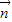
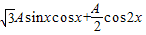
=A（
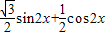）=Asin（2x+
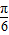）．因为A＞0，由题意可知A=6．
（Ⅱ）由（Ⅰ）f（x）=6sin（2x+
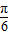）．将函数y=f（x）d的图象向左平移
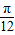个单位后得到，y=6sin[2（x+
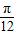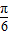）+]=6sin（2x+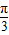）．的图象．再将所得图象各点的横坐标缩短为原来的倍，纵坐标不变，得到函数y=6sin（4x+
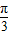）的图象．因此g（x）=6sin（4x+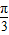）．因为x∈[0，
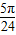]，所以4x+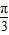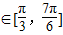，故g（x）在[0，
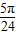]上的值域为[-3，6]．点评：本题考查三角函数的最值，平面向量数量积的坐标表示、模、夹角，正弦函数的定义域和值域，函数y=Asin（ωx+φ）的图象变换，考查计算能力．
练习册系列答案
相关题目
已知向量
=（sinx，cosx），向量
=(1，
)，则|
+
|的最大值为（ ）
| a |
| b |
| 3 |
| a |
| b |
| A、3 | ||
B、
| ||
| C、1 | ||
| D、9 |