题目内容
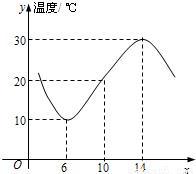
如右图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+B,(0≤φ<2π),则温度变化曲线的函数解析式为 .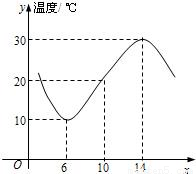
【答案】分析:由图可以看出函数的半个周期是8,可求得ω最高点坐标是(14,30),最低点坐标是(6,10),由公式可求得A,B,再将点(6,10)代入即可求得符合题意的三角函数解析式.
解答:解:图中从6时到14时的图象是函数y=Asin(ωx+∅)+B的半个周期的图象,
∴ •
• =14-6⇒ω=
=14-6⇒ω= .
.
又由图可得A= =10,B=
=10,B= =20.
=20.
∴y=10sin( x+∅)+20.
x+∅)+20.
将x=6,y=10代入上式,得sin( π+∅)=-1.
π+∅)=-1.
∴ π+∅=
π+∅= π⇒∅=
π⇒∅= π.
π.
故所求曲线的解析式为y=10sin( x+
x+ π)+20,x∈[6,14].
π)+20,x∈[6,14].
故答案为y=10sin( x+
x+ π)+20,
π)+20,
点评:此类“由已知条件或图象求函数的解析式”的题目,实质上是用“待定系数法”确定A,ω,∅和B,它们的计算方法为
A= ,B=
,B= .ω与周期有关,可通过T=
.ω与周期有关,可通过T= 求得,而关键的一步在于如何确定∅.通常是将图象上已知点的坐标代入函数解析式,得到一个关于φ的简单三角方程,但∅到底取何值却值得考虑.若得方程sin∅=
求得,而关键的一步在于如何确定∅.通常是将图象上已知点的坐标代入函数解析式,得到一个关于φ的简单三角方程,但∅到底取何值却值得考虑.若得方程sin∅= ,那么∅是取
,那么∅是取 ,还是取
,还是取 呢?这就要看所代入的点是在上升的曲线上,还是在下降的曲线上了.若在上升的曲线上,∅就取
呢?这就要看所代入的点是在上升的曲线上,还是在下降的曲线上了.若在上升的曲线上,∅就取 ,否则就取
,否则就取 ,而不能同时取两个值.
,而不能同时取两个值.
解答:解:图中从6时到14时的图象是函数y=Asin(ωx+∅)+B的半个周期的图象,
∴
 •
• =14-6⇒ω=
=14-6⇒ω= .
.又由图可得A=
 =10,B=
=10,B= =20.
=20.∴y=10sin(
 x+∅)+20.
x+∅)+20.将x=6,y=10代入上式,得sin(
 π+∅)=-1.
π+∅)=-1.∴
 π+∅=
π+∅= π⇒∅=
π⇒∅= π.
π.故所求曲线的解析式为y=10sin(
 x+
x+ π)+20,x∈[6,14].
π)+20,x∈[6,14].故答案为y=10sin(
 x+
x+ π)+20,
π)+20,点评:此类“由已知条件或图象求函数的解析式”的题目,实质上是用“待定系数法”确定A,ω,∅和B,它们的计算方法为
A=
 ,B=
,B= .ω与周期有关,可通过T=
.ω与周期有关,可通过T= 求得,而关键的一步在于如何确定∅.通常是将图象上已知点的坐标代入函数解析式,得到一个关于φ的简单三角方程,但∅到底取何值却值得考虑.若得方程sin∅=
求得,而关键的一步在于如何确定∅.通常是将图象上已知点的坐标代入函数解析式,得到一个关于φ的简单三角方程,但∅到底取何值却值得考虑.若得方程sin∅= ,那么∅是取
,那么∅是取 ,还是取
,还是取 呢?这就要看所代入的点是在上升的曲线上,还是在下降的曲线上了.若在上升的曲线上,∅就取
呢?这就要看所代入的点是在上升的曲线上,还是在下降的曲线上了.若在上升的曲线上,∅就取 ,否则就取
,否则就取 ,而不能同时取两个值.
,而不能同时取两个值. 
练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
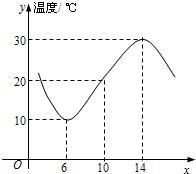 如右图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+B,(0≤φ<2π),则温度变化曲线的函数解析式为
如右图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+B,(0≤φ<2π),则温度变化曲线的函数解析式为