题目内容
(本题满分12分)已知圆C经过点 ,且圆心
,且圆心 在直线
在直线 上
上
(1)求圆 的方程;
的方程;
(2)过点 的直线
的直线 截圆所得弦长为
截圆所得弦长为 ,求直线
,求直线 的方程
的方程
(1)
(2) 或
或
【解析】
试题分析:
(1)由圆心 在直线
在直线 上,可设圆心C(
上,可设圆心C( ),再根据
),再根据 求出
求出 即可确定圆C的方程.
即可确定圆C的方程.
(2)用点斜式设直线方程,但要考虑斜率存在与不存在两种情况,当斜率存在时设直线方程为 ,由圆心到直线的距离
,由圆心到直线的距离 可求
可求 .
.
试题解析:(1)设圆心C( ),(1分)
),(1分)
 (4分)
(4分)
所以 (5分),
(5分),
圆C的方程为 (6分)
(6分)
(2)若直线 的斜率不存在,方程为
的斜率不存在,方程为 ,此时直线
,此时直线 截圆所得弦长为
截圆所得弦长为 ,符合题意;若直线
,符合题意;若直线 的斜率存在,设方程为
的斜率存在,设方程为
由题意,圆心到直线的距离

直线 的方程为
的方程为
综上,所求方程为 或
或
考点:1圆的方程;2直线与圆.
考点分析: 考点1:直线和圆的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
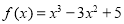 的单调减区间是( )
的单调减区间是( ) 的图象,只需把函数
的图象,只需把函数 的图象上所有的点
的图象上所有的点 倍,再向左平移
倍,再向左平移 个单位长度;
个单位长度; 倍,再向左平移
倍,再向左平移 个单位长度;
个单位长度; 个单位长度;
个单位长度; 个单位长度。
个单位长度。 是偶函数,则此函数的图象与y轴交点的纵坐标的最大值为( )
是偶函数,则此函数的图象与y轴交点的纵坐标的最大值为( ) C.4 D.-2
C.4 D.-2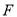 是抛物线
是抛物线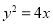 的焦点,点
的焦点,点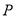 在该抛物线上,且点
在该抛物线上,且点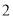 ,则
,则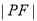 =( )
=( )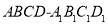 的底面是边长为1的正方形,侧棱长
的底面是边长为1的正方形,侧棱长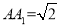 ,则异面直线
,则异面直线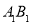 与
与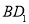 的夹角大小等于
的夹角大小等于 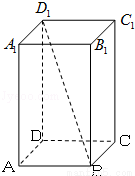
 ,
, ”是真命题,则实数
”是真命题,则实数 的取值范围为 .
的取值范围为 . 的最小值为 ☆
的最小值为 ☆