题目内容
函数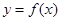 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( )
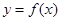 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( )A.若函数在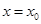 时取得极值,则 时取得极值,则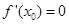 |
B.若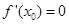 ,则函数在 ,则函数在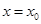 处取得极值 处取得极值 |
C.若在定义域内恒有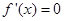 ,则 ,则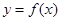 是常数函数 是常数函数 |
D.函数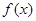 在 在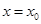 处的导数是一个常数 处的导数是一个常数 |
B.
试题分析:对于B,可以构造函数
 ,则
,则 ,而
,而 并不是
并不是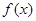 的极值点,而A,C,D均正确,∴选B.
的极值点,而A,C,D均正确,∴选B.
练习册系列答案
相关题目
 (
( 是常数)在
是常数)在 处的切线方程为
处的切线方程为 ,且
,且 .
. (
( )在区间
)在区间 内不是单调函数,求实数
内不是单调函数,求实数 的取值范围.
的取值范围.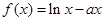 ,
,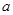 为常数.
为常数.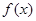 在
在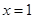 处的切线与
处的切线与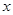 轴平行,求
轴平行,求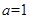 时,试比较
时,试比较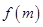 与
与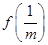 的大小;
的大小;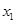 、
、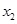 ,试证明
,试证明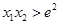 .
.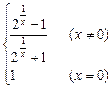
 ,若
,若 ,则
,则 ,
, ,
, 的大小关系为( )
的大小关系为( )



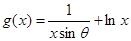 在
在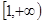 上为增函数,
上为增函数,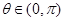 ,
,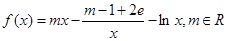
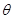 的值;
的值;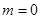 时,求函数
时,求函数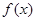 的单调区间和极值;
的单调区间和极值;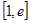 上至少存在一个
上至少存在一个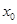 ,使得
,使得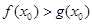 成立,求
成立,求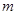 的取值范围.
的取值范围.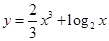 ;
;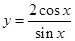 .
.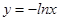 在点
在点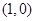 处的切线斜率为 .
处的切线斜率为 .