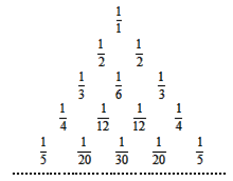题目内容
设函数 ,数列
,数列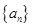 满足
满足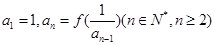 .
.
⑴求数列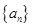 的通项公式;
的通项公式;
⑵设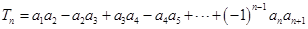 ,若
,若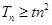 对
对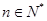 恒成立,求实数
恒成立,求实数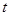 的取值范围;
的取值范围;
⑶是否存在以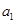 为首项,公比为
为首项,公比为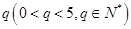 的数列
的数列 ,
,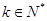 ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列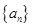 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.
 ,数列
,数列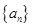 满足
满足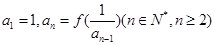 .
.⑴求数列
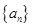 的通项公式;
的通项公式;⑵设
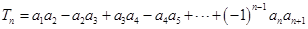 ,若
,若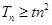 对
对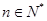 恒成立,求实数
恒成立,求实数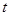 的取值范围;
的取值范围;⑶是否存在以
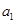 为首项,公比为
为首项,公比为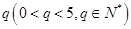 的数列
的数列 ,
,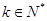 ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列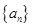 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.(1) ;(2)
;(2)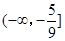 ;(3)存在,理由详见解析.
;(3)存在,理由详见解析.
 ;(2)
;(2)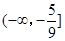 ;(3)存在,理由详见解析.
;(3)存在,理由详见解析.试题分析:(1)将
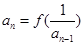 利用
利用 进行化简,得到关于
进行化简,得到关于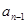 与
与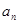 的递推关系式,根据其特点,求其通项公式;(2)本题关键是求出
的递推关系式,根据其特点,求其通项公式;(2)本题关键是求出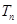 ,根据其表达式的特点,可每两项组合后提取公因式
,根据其表达式的特点,可每两项组合后提取公因式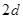 后,转化为等差数列求和,但要注意对
后,转化为等差数列求和,但要注意对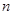 ,分奇偶性讨论,求出
,分奇偶性讨论,求出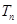 后,
后,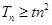 对
对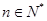 恒成立再分离参数后转化为求最值问题,容易求出实数
恒成立再分离参数后转化为求最值问题,容易求出实数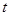 的取值范围;(3)此类问题,一般先假设存在符合条件的数列,解出来则存在,如果得到矛盾的结果,则假设错误,这样的数列则不存在.
的取值范围;(3)此类问题,一般先假设存在符合条件的数列,解出来则存在,如果得到矛盾的结果,则假设错误,这样的数列则不存在.试题解析:⑴因为
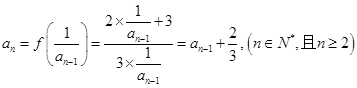 ,
,所以
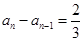 . 2分
. 2分因为
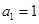 ,所以数列
,所以数列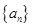 是以1为首项,公差为
是以1为首项,公差为 的等差数列.
的等差数列.所以
 . 4分
. 4分⑵①当
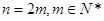 时,
时,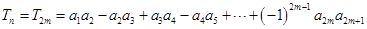
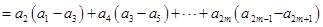

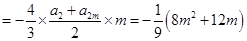
 . 6分
. 6分②当
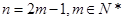 时,
时,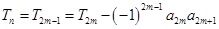
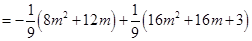
 . 8分
. 8分所以
 要使
要使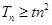 对
对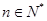 恒成立,
恒成立,只要使

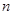 为偶数恒成立.
为偶数恒成立.只要使
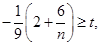 ,
,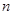 为偶数恒成立,故实数
为偶数恒成立,故实数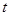 的取值范围为
的取值范围为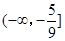 . 10分
. 10分⑶由
 ,知数列
,知数列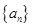 中每一项都不可能是偶数.
中每一项都不可能是偶数.①如存在以
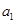 为首项,公比
为首项,公比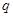 为2或4的数列
为2或4的数列 ,
,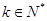 ,
,此时
 中每一项除第一项外都是偶数,故不存在以
中每一项除第一项外都是偶数,故不存在以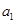 为首项,公比为偶数的数列
为首项,公比为偶数的数列 . 12分
. 12分②当
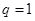 时,显然不存在这样的数列
时,显然不存在这样的数列 .
.当
 时,若存在以
时,若存在以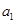 为首项,公比为3的数列
为首项,公比为3的数列 ,
,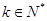 .
.则
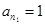 ,
,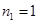 ,
,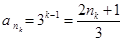 ,
,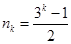 .
.所以满足条件的数列
 的通项公式为
的通项公式为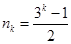 . 16分
. 16分
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
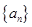 和等比数列
和等比数列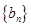 中,a1=2, 2b1=2, b6=32,
中,a1=2, 2b1=2, b6=32, 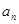 和
和 ;
;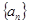 的前n项和
的前n项和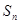 ,已知对任意的
,已知对任意的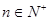 ,点
,点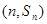 均在函数
均在函数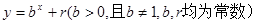 的图像上.
的图像上.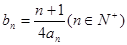 ,求数列
,求数列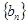 的前n项和
的前n项和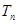 .
.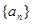 中,各项都是正数,且
中,各项都是正数,且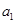 ,
,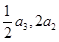 成等差数列,则
成等差数列,则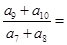 ( )
( )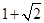
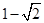
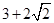
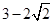
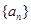 的前n项和为
的前n项和为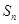 ,若
,若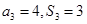 ,则公差
,则公差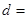 ___________.
___________.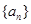 公比为
公比为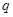 ,其前
,其前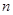 项和为
项和为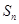 ,若
,若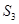 、
、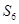 、
、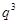 等于( )
等于( )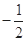
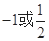
 排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )
排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )
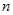 行有
行有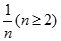 ,每个数是它下一行左右相邻两数的和,如:
,每个数是它下一行左右相邻两数的和,如: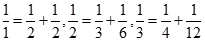 …,则第
…,则第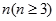 行第3个数字是 .
行第3个数字是 .