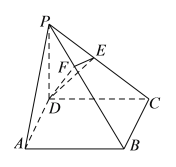
题目内容
【题目】已知椭圆![]()
![]() 的左焦点
的左焦点![]() 左顶点
左顶点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知![]() ,
,![]() 是椭圆上的两点,
是椭圆上的两点,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.若
两侧的动点.若![]() ,试问直线
,试问直线![]() 的斜率是否为定值?请说明理由.
的斜率是否为定值?请说明理由.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)根据条件依次求得![]() ,
,![]() 和
和![]() ,从而可得方程;
,从而可得方程;
(Ⅱ)当∠APQ=∠BPQ,则PA、PB的斜率之和为0,设直线PA的斜率为k,则PB的斜率为-k,PA的直线方程为y-3=k(x-2),PB的直线方程为y-9=-k(x-2),由此利用韦达定理结合已知条件能求出AB的斜率为定值![]() .
.
详解:(Ⅰ)由题意可得,![]() ,
,![]() 由
由![]() ,得
,得![]()
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)当![]() 时,
时,![]() ,
,![]() 的斜率之和为
的斜率之和为![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,设
,设![]()
![]() ,
,![]() 的方程为
的方程为![]() .
.
联立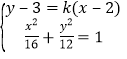 消
消![]() 得
得
![]() .
.
所以![]()
同理![]()
所以![]() ,
,![]() .
.
所以![]() .
.
所以![]() 的斜率为定值
的斜率为定值![]()

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】兰天购物广场某营销部门随机抽查了100名市民在2018年国庆长假期间购物广场的消费金额,所得数据如表,已知消费金额不超过3千元与超过3千元的人数比恰为![]() .
.
消费金额(单位:千元) | 人数 | 频率 |
| 8 | 0.08 |
| 12 | 0.12 |
|
|
|
|
|
|
| 8 | 0.08 |
| 7 | 0.07 |
合计 | 100 | 1.00 |

(1)试确定![]() ,
,![]() ,
,![]() ,
,![]() 的值,并补全频率分布直方图(如图);
的值,并补全频率分布直方图(如图);
(2)用分层抽样的方法从消费金额在![]() 、
、![]() 和
和![]() 的三个群体中抽取7人进行问卷调查,则各小组应抽取几人?若从这7人中随机选取2人,则此2人来自同一群体的概率是多少?
的三个群体中抽取7人进行问卷调查,则各小组应抽取几人?若从这7人中随机选取2人,则此2人来自同一群体的概率是多少?