题目内容

14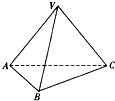．如图，三棱锥V-ABC的底面为正三角形，侧面VAC与底面垂直，且VA=VC，已知其侧（左）视图的面积为$\sqrt{3}$，其正（主）视图的面积为2．

分析 由三视图的画图要求“长对正，高平齐，宽相等”可以找出左视图的宽、高与俯视图的宽、主视图的高的相等关系，进而求出答案．

解答 解：设底面正△ABC的边长为a，侧面VAC的底边AC上的高为h，可知底面正△ABC的高为$\frac{\sqrt{3}}{2}$a，
∵左视图的高与主视图的高相等，
∴左视图的高是h，
又左视图的宽是底面△ABC的边AC上的高$\frac{\sqrt{3}}{2}$a，
∴S左视图=$\frac{1}{2}×$$\frac{\sqrt{3}}{2}$a×h=$\sqrt{3}$．
∴ah=4
∵其主视图为△VAC，∴$\frac{1}{2}$ah=2
故答案为：2．

点评 本题考查了三视图的有关计算，正确理解三视图的画图要求是解决问题的关键．

练习册系列答案
相关题目
8．解不等式：2x-x2≥-1．
9．已知集合M={y|y=2x2+1，x∈R }，N={x∈R|y=$\sqrt{1-x}+1$}，则M∪N=R，M∩N={1}．
2．设集合P={-1，0，1}，Q={x|$\sqrt{x}$＜$\sqrt{2}$}，则P∩Q=（　　）
A．{0，1}B．{1}C．{0}D．{-1，0，1}
9．在某次考试中，共有10道题供选择，已知该生会答其中的6道题，随机从中抽5道题供该生回答，答对3道题则及格，求该生在第一题不回答的情况下及格的概率．
19．已知四边形ABCD，$\overrightarrow{AB}$=$\overrightarrow{DC}$=（1，1），$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}$=$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$，则四边形ABCD的面积为（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2
6．已知点A（-2，0），B（2，0），动点P满足|$\overrightarrow{PB}$|，$\frac{1}{2}$|$\overrightarrow{PA}$|，2$\sqrt{3}$成等差数列．
（1）证明动点P的轨迹是双曲线，并求出双曲线的方程；
（2）若直线y=kx+m（k≠0．m≠0）与双曲线交于不同的两个点C，D，且C，D两点都在以Q（0，-1）为圆心的同一圆上，求m的取值范围．
3．设an=$\frac{1}{n}$sin$\frac{nπ}{5}$，Sn=a1+a2+…+an，在S1，S2，…，S2014中，正数的个数是（　　）
A．806B．1007C．1612D．2014
4．若2a+3b≤2-b+3-a，则a+b≤0（填“＜”“＞0”或“=”）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网