题目内容
11．已知集合A={x|-2≤x≤2}，B={x|a+1＜x＜2a-3}，若A∪B=A，求实数a的取值范围．分析 根据A与B的并集为A，得到B为A的子集，列出关于a的不等式，求出不等式的解集即可求出a的范围．
解答 解：∵A∪B=A，∴B⊆A，
由A={x|-2≤x≤2}，B={x|a+1＜x＜2a-3}，
分两种情况考虑：当B=∅时，则有2a-3≤a+1，
解得：a≤4，满足题意；
当B≠∅时，则有$\left\{\begin{array}{l}{2a-3＞a+1}\\{a+1≥-2}\\{2a-3≤2}\end{array}\right.$，无解，
综上，a的取值范围为a≤4
点评 此题考查了并集及其运算，熟练掌握并集的定义是解本题的关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
2．
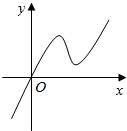已知函数f（x）的定义域为R，且满足f（4）=1，f′（x）为f（x）的导函数，又知y=f′（x）的图象如图所示，若两个正数a，b满足，f（2a+b）＜1，则$\frac{b+2}{a+1}$的取值范围是（ ）
已知函数f（x）的定义域为R，且满足f（4）=1，f′（x）为f（x）的导函数，又知y=f′（x）的图象如图所示，若两个正数a，b满足，f（2a+b）＜1，则$\frac{b+2}{a+1}$的取值范围是（ ）| A． | $（{\frac{2}{3}，6}）$ | B． | $[{\frac{2}{3}，6}]$ | C． | $[\frac{1}{4}，\frac{5}{2}]$ | D． | $（{\frac{1}{4}，\frac{5}{2}}）$ |
6．函数y=$\sqrt{2-3x}$-（x+1）0的定义域为（ ）
| A． | （-1，$\frac{2}{3}$] | B． | （-1，$\frac{2}{3}$） | C． | （-∞，-1）∪（-1，$\frac{2}{3}$] | D． | [$\frac{2}{3}$，+∞） |
16．函数f（x）=log2（4+3x-x2）的单调递减区间是（ ）
| A． | （-∞，$\frac{3}{2}$] | B． | [$\frac{3}{2}$，+∞） | C． | （-1，$\frac{3}{2}$] | D． | [$\frac{3}{2}$，4） |
3．某学校有老师200人，男学生1200人，女学生1000人，现用分层抽样的方法从全体师生中抽取一个容量为n的样本，已知女学生一共抽取了80人，则n的值是（ ）
| A． | 193 | B． | 192 | C． | 191 | D． | 190 |
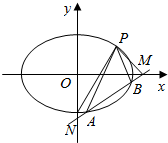如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{3}}}{2}$，过椭圆C上一点P（2，1）作倾斜角互补的两条直线，分别与椭圆交于点A、B，直线AB与x轴交于点M，与y轴负半轴交于点N．