题目内容
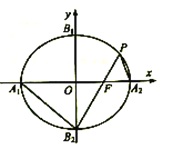
【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,![]() 两点为喷泉,圆心
两点为喷泉,圆心![]() 为
为![]() 的中点,其中
的中点,其中![]() 米,半径
米,半径![]() 米,市民可位于水池边缘任意一点
米,市民可位于水池边缘任意一点![]() 处观赏.
处观赏.
(1)若当![]() 时,
时,![]() ,求此时
,求此时![]() 的值;
的值;
(2)设![]() ,且
,且![]() .
.
(i)试将![]() 表示为
表示为![]() 的函数,并求出
的函数,并求出![]() 的取值范围;
的取值范围;
(ii)若同时要求市民在水池边缘任意一点![]() 处观赏喷泉时,观赏角度
处观赏喷泉时,观赏角度![]() 的最大值不小于
的最大值不小于![]() ,试求
,试求![]() 两处喷泉间距离的最小值.
两处喷泉间距离的最小值.
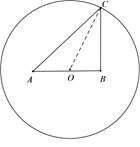
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ,
,![]() ;(ii)
;(ii)![]() .
.
【解析】
(1)在![]() 中,由正弦定理可得所求;
中,由正弦定理可得所求;
(2)(i)由余弦定理得![]() ,两式相加可得所求解析式.(ii)在
,两式相加可得所求解析式.(ii)在![]() 中,由余弦定理可得
中,由余弦定理可得![]() ,根据
,根据![]() 的最大值不小于
的最大值不小于![]() 可得关于
可得关于![]() 的不等式,解不等式可得所求.
的不等式,解不等式可得所求.
(1)在![]() 中,由正弦定理得
中,由正弦定理得![]() ,
,
所以 ,
,
即![]() .
.
(2)(i)在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
又![]()
所以![]() ,
,
即![]() .
.
又![]() ,解得
,解得![]() ,
,
所以所求关系式为![]() ,
,![]() .
.
(ii)当观赏角度![]() 的最大时,
的最大时,![]() 取得最小值.
取得最小值.
在![]() 中,由余弦定理可得
中,由余弦定理可得
![]() ,
,
因为![]() 的最大值不小于
的最大值不小于![]() ,
,
所以![]() ,解得
,解得![]() ,
,
经验证知![]() ,
,
所以![]() .
.
即![]() 两处喷泉间距离的最小值为
两处喷泉间距离的最小值为![]() .
.

练习册系列答案
相关题目