Question

已知圆在两坐标轴上的四个截距之和为2,且经过两点P(4,2)、Q(-1,3),求此圆方程.

Answer 1

解析：设所求圆的方程为x²+y²+Dx+Ey+F=0.?

因为P(4,2)、Q(-1,3)两点在圆上,?

所以4D+2E+F+20=0,                                      ①?

-D+3E+F+10=0.                                              ②?

又圆在两坐标轴上的四个截距之和为2,则由

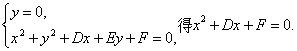
所以x₁+x₂=-D.?

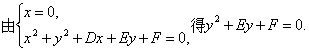
所以y₁+y₂=-E.?

所以-D-E=2.                                                   ③?

解①②③得D=-2,E=0,F=-12.?

故所求圆的方程为x²+y²-2x-12=0.