题目内容
如图,已知圆![]()
![]() 是椭圆
是椭圆![]() 的内接△
的内接△![]() 的内切圆, 其中
的内切圆, 其中![]() 为椭圆的左顶点.
为椭圆的左顶点.
(1)求圆![]() 的半径
的半径![]() ;
;
(2)过点![]() 作圆
作圆![]() 的两条切线交椭圆于
的两条切线交椭圆于![]() 两点,判断直线
两点,判断直线![]() 与圆
与圆![]() 的位置关系并说明理由.
的位置关系并说明理由.

|
解: (1)设![]()
![]() ,过圆心
,过圆心![]() 作
作![]() 于
于![]() ,
,![]() 交长轴于
交长轴于![]()
由![]() 得
得![]() ,即
,即 ![]() (1)
(1)
而点![]()
![]() 在椭圆上,
在椭圆上,![]() (2)
(2)
由(1)、 (2)式得![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
(2) 设过点![]() 与圆
与圆![]() 相切的直线方程为:
相切的直线方程为:![]() (3)
(3)
则![]() ,即
,即![]() (4)
(4)
解得![]()
将(3)代入![]() 得
得![]() ,则异于零的解为
,则异于零的解为![]()
设![]() ,
,![]() ,则
,则![]()
则直线![]() 的斜率为:
的斜率为:![]()
于是直线![]() 的方程为:
的方程为:![]() 即
即![]()
则圆心![]() 到直线
到直线![]() 的距离
的距离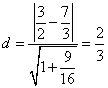 故结论成立.
故结论成立.

练习册系列答案
相关题目

 如图,已知圆
如图,已知圆 如图,已知圆
如图,已知圆
 是椭圆
是椭圆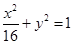 的内接△
的内接△ 的内切圆, 其中
的内切圆, 其中 为椭圆的左顶点.
为椭圆的左顶点.
 的半径
的半径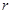 ;
; 作圆
作圆 两点,
两点,
 与圆
与圆 如图,已知圆
如图,已知圆
 是椭圆
是椭圆 的内接△
的内接△ 的内切圆, 其中
的内切圆, 其中 为椭圆的左顶点.
为椭圆的左顶点.  的半径
的半径 ;
; 作圆
作圆 两点,
两点, 与圆
与圆