题目内容
已知函数
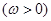 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减;如图,四边形
上单调递减;如图,四边形 中,
中, ,
, ,
, 为
为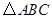 的内角
的内角 的对边,
的对边,
且满足 .
.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,设
,设 ,
, ,
, ,求四边形
,求四边形 面积的最大值.
面积的最大值.
(1)正弦定理的运用根据边角的转换来得到证明。
(2)  时取最大值,
时取最大值, 的最大值为
的最大值为
解析试题分析:解:(Ⅰ)由题意知: ,解得:
,解得: , 2分
, 2分


 4分
4分 6分
6分
(Ⅱ)因为 ,所以
,所以 ,所以
,所以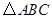 为等边三角形
为等边三角形 8分
8分
 , 10分
, 10分 ,
, ,
,
当且仅当 即
即 时取最大值,
时取最大值, 的最大值为
的最大值为 12分
12分
考点:解三角形以及三角函数性质的运用
点评:解决的关键是利用三角函数的性质得到最值,属于基础题。

练习册系列答案
相关题目
 中,
中,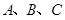 是三角形的三内角,
是三角形的三内角,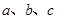 是三内角对应的三边,已知
是三内角对应的三边,已知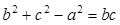 。
。 的大小;
的大小;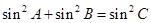 ,求角
,求角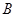 的大小。
的大小。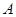 相距20
相距20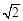 海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东
海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东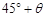
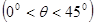 的C处,
的C处,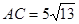 .在离观测站A的正南方某处E,
.在离观测站A的正南方某处E,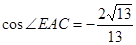
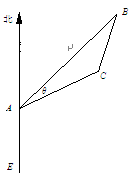
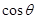 ; (2)求该船的行驶速度v(海里/小时);
; (2)求该船的行驶速度v(海里/小时);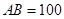 米,如图,同时也能测量出
米,如图,同时也能测量出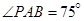 ,
,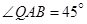 ,
,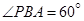 ,
,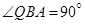 ,则P、Q两棵树和A、P两棵树之间的距离各为多少?
,则P、Q两棵树和A、P两棵树之间的距离各为多少?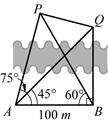
 中,三个内角
中,三个内角 所对的边分别是
所对的边分别是
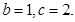
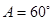 ,求
,求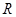
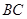 边上的中线长为
边上的中线长为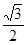 ,求
,求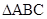 的面积。
的面积。 中,角
中,角 的对边分别为
的对边分别为 ,
,
 ,
,
 ,且
,且
 的值; (2) 若
的值; (2) 若 ,
,  , 求
, 求 的值.
的值. 中,
中,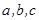 分别是角A、B、C的对边,且满足:
分别是角A、B、C的对边,且满足: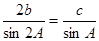 .
.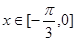 时,求函数
时,求函数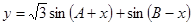 的值域.
的值域.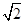 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10