题目内容
已知α是△ABC的一个内角,且sinα+cosα=
,则sin2α+cos2α的值为
| 1 |
| 5 |
-
| 3 |
| 5 |
-
.| 3 |
| 5 |
分析:由α∈(0,π),sinα+cosα=
∈(0,1)可知α为钝角,易求sin2α=-
,从而可求sinα-cosα=
,于是易求cosα=-
及答案.
| 1 |
| 5 |
| 24 |
| 25 |
| 7 |
| 5 |
| 3 |
| 5 |
解答:解:∵α∈(0,π),sinα+cosα=
,①
∴sin2α+cos2α+2sinαcosα=
,
∴2sinαcosα=
-1=-
<0,
又sinα>0,
∴cosα<0,
∴sinα-cosα>0,
又(sinα-cosα)2=1-2sinαcosα=1-(-
)=
,
∴sinα-cosα=
,②
由①②得:cosα=-
,sinα=
.
∴sin2α+cos2α=
-sin2α=
=-
.
故答案为:-
.
| 1 |
| 5 |
∴sin2α+cos2α+2sinαcosα=
| 1 |
| 25 |
∴2sinαcosα=
| 1 |
| 25 |
| 24 |
| 25 |
又sinα>0,
∴cosα<0,
∴sinα-cosα>0,
又(sinα-cosα)2=1-2sinαcosα=1-(-
| 24 |
| 25 |
| 49 |
| 25 |
∴sinα-cosα=
| 7 |
| 5 |
由①②得:cosα=-
| 3 |
| 5 |
| 4 |
| 5 |
∴sin2α+cos2α=
| 1 |
| 25 |
| 1-16 |
| 25 |
| 3 |
| 5 |
故答案为:-
| 3 |
| 5 |
点评:本题考查三角函数的恒等变换及化简求值,求得sinα-cosα=
是关键,也是难点,考查方程思想与运算能力,属于中档题.
| 7 |
| 5 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
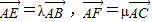 ,则
,则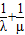 = .
= .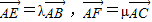 ,则
,则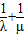 = .
= .