Question

如图,已知平行六面体ABCD—A₁B₁C₁D₁的底面为正方形,O₁、O分别为上、下底面的中心,且A₁在底面ABCD上的射影是O.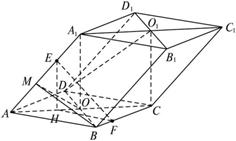

(1)求证:平面O₁DC⊥平面ABCD;

(2)若点E、F分别在棱AA₁、BC上,且AE=2EA₁,问点F在何处时,EF⊥AD?

(3)若∠A₁AB=60°,求二面角CAA₁B的大小.(用反三角函数表示)

Answer 1

(1)证明:连结AC、BD、A₁C₁,则O为AC、BD的交点,

O₁为A₁C₁、B₁D₁的交点.

由平行六面体的性质知A₁O₁∥OC且A₁O₁=OC,

∴四边形A₁OCO₁为平行四边形,

A₁O∥O₁C.

又∵A₁O⊥平面ABCD,

∴O₁C⊥平面ABCD.

又∵O₁C平面O₁DC,

∴平面O₁DC⊥平面ABCD.

(2)解:作EH⊥平面ABCD,垂足为H,

则EH∥A₁O,点H在直线AC上,

且EF在平面ABCD上的射影为HF.

由三垂线定理及其逆定理,知EF⊥ADFH∥AB.

∵AE=2EA₁,∴AH=2HO,

从而CH=2AH.

又∵HF∥AB,∴CF=2BF.

从而EF⊥ADCF=2BF,

∴当F为BC的三等分点(靠近B)时,有EF⊥AD.

(3)解:过点O作OM⊥AA₁,垂足为M,连结BM.

∵A₁O⊥平面ABCD,∴A₁O⊥OB.

又∵OB⊥OA,∴OB⊥平面A₁AO.

由三垂线定理得AA₁⊥MB.

∴∠OMB为二面角CAA₁B的平面角.

在Rt△AMB中,∠MAB=60°,

∴MB=AB.

又∵BO=AB,∴sin∠OMB=.

∴∠OMB=arcsin.

二面角C-AA₁-B的大小为arcsin.