题目内容
已知函数f(x)=
x3-
ax2-3x.
(1)若f(x)在x=3处有极值,求a的值;
(2)在(1)的条件下,求f(x)在区间[0,4]上的最大值.
| 1 |
| 3 |
| 1 |
| 2 |
(1)若f(x)在x=3处有极值,求a的值;
(2)在(1)的条件下,求f(x)在区间[0,4]上的最大值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:综合题,导数的概念及应用
分析:(1)由题意得f'(3)=9-3a-3=0,解出a后检验即可;
(2)利用导数求得函数的极值、断点处函数值,其中最大者即为最大值;
(2)利用导数求得函数的极值、断点处函数值,其中最大者即为最大值;
解答:
解:(1)f'(x)=x2-ax-3.
∵f(x)在x=3处有极值,∴f'(3)=9-3a-3=0,即a=2.
∴f'(x)=x2-2x-3=(x+1)(x-3).
当x∈(-1,3)时,f'(x)<0,当x∈(3,+∞)时,f'(x)>0,
∴f(x)在x=3处取得极值时,a=2.
(2)在(1)的条件下,f(x)=
x3-x2-3x,f′(x)=x2-2x-3,
令f′(x)=0,得x=-1或x=3,
由(1)知函数f(x)在x=-1和x=3处有极值.
又f(0)=0,f(3)=-9,f(4)=-
,
∴f(x)在区间[0,4]上的最大值为f(0)=0.
∵f(x)在x=3处有极值,∴f'(3)=9-3a-3=0,即a=2.
∴f'(x)=x2-2x-3=(x+1)(x-3).
当x∈(-1,3)时,f'(x)<0,当x∈(3,+∞)时,f'(x)>0,
∴f(x)在x=3处取得极值时,a=2.
(2)在(1)的条件下,f(x)=
| 1 |
| 3 |
令f′(x)=0,得x=-1或x=3,
由(1)知函数f(x)在x=-1和x=3处有极值.
又f(0)=0,f(3)=-9,f(4)=-
| 20 |
| 3 |
∴f(x)在区间[0,4]上的最大值为f(0)=0.
点评:该题考查利用导数研究函数的极值、最值,正确理解导数与函数极值、最值的关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
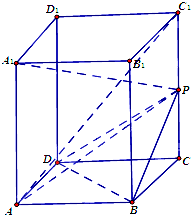 如图,在直四棱柱ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱C1C垂直于底面ABCD,且C1C=2,点P是侧棱C1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱C1C垂直于底面ABCD,且C1C=2,点P是侧棱C1C的中点.