题目内容
(2009•台州一模)已知数列{an}的首项a1=
,前n项和Sn=n2an.
(Ⅰ)求证:an+1=
an;
(Ⅱ)记bn=lnSn,Tn为{bn}的前n项和,求e-Tn-n的值.
| 1 |
| 2 |
(Ⅰ)求证:an+1=
| n |
| n+2 |
(Ⅱ)记bn=lnSn,Tn为{bn}的前n项和,求e-Tn-n的值.
分析:(Ⅰ)由Sn=n2an①,得Sn+1=(n+1)2an+1②,②-①后整理可得结论;
(Ⅱ)利用累积法求出an,从而得到Sn,进而求得bn,Tn,利用对数恒等式可得答案;
(Ⅱ)利用累积法求出an,从而得到Sn,进而求得bn,Tn,利用对数恒等式可得答案;
解答:解:(Ⅰ)由Sn=n2an①,得Sn+1=(n+1)2an+1②,
②-①得:an+1=(n+1)2an+1-n2an,
整理得,an+1=
an.
(Ⅱ)由an+1=
an,得
=
,
所以an=a1×
×
×…×
=
×
×
×…×
×
=
(n≥2),
又当n=1时,a1=
,所以an=
.
∴Sn=n2an=
,bn=lnSn=lnn-ln(n+1),
∴Tn=(ln1-ln2)+(ln2-ln3)+(ln3-ln4)+…+(lnn-ln(n+1))=-ln(n+1),
∴e-Tn-n=eln(n+1)-n=1.
②-①得:an+1=(n+1)2an+1-n2an,
整理得,an+1=
| n |
| n+2 |
(Ⅱ)由an+1=
| n |
| n+2 |
| an+1 |
| an |
| n |
| n+2 |
所以an=a1×
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 4 |
| n-2 |
| n |
| n-1 |
| n+1 |
=
| 1 |
| n(n+1) |
又当n=1时,a1=
| 1 |
| 2 |
| 1 |
| n(n+1) |
∴Sn=n2an=
| n |
| n+1 |
∴Tn=(ln1-ln2)+(ln2-ln3)+(ln3-ln4)+…+(lnn-ln(n+1))=-ln(n+1),
∴e-Tn-n=eln(n+1)-n=1.
点评:本题考查由数列递推公式求数列通项、数列求和,考查学生逻辑推理能力、运算能力,属中档题.

练习册系列答案
相关题目
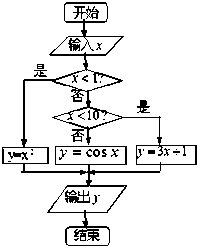 (2009•台州一模)根据右边程序框图,若输出y的值是4,则输入的实数x=
(2009•台州一模)根据右边程序框图,若输出y的值是4,则输入的实数x=