题目内容
A地某单位用三辆客车送职工去B地旅游,从A地到B地有高速公路和一级公路各一条,已知客车走一级公路堵车的概率为 ;若1号、2号两辆客车走一级公路,3号公路走高速公路,且在辆客车是否被堵车相互之间无影响,若三辆客车中恰有一辆被堵车的概率为
;若1号、2号两辆客车走一级公路,3号公路走高速公路,且在辆客车是否被堵车相互之间无影响,若三辆客车中恰有一辆被堵车的概率为 .
.
(I)求客车走高速公路被堵车的概率;
(II)求三辆客车中被堵车辆的辆数ξ的数学期望和方差.
解:(I)客车走一级公路堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ,
,
设客车走高速公路堵车的概率是p,不堵车的概率是1-p,
∴ ,
,
解得p= .
.
(II)ξ可能的取值是0,1,2,3,
p(ξ=0)= =
=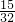 ,
,
p(ξ=1)= ,
,
p(ξ=2)= ,
,
p(ξ=3)= ,
,
∴Eξ=0× ,
,
Dξ= +
+ .
.
分析:(I)客车走一级公路堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ,设客车走高速公路堵车的概率是p,不堵车的概率是1-p,由题设知
,设客车走高速公路堵车的概率是p,不堵车的概率是1-p,由题设知 ,从而得到客车走高速公路被堵车的概率.
,从而得到客车走高速公路被堵车的概率.
(II)ξ可能的取值是0,1,2,3,p(ξ=0)=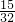 ,p(ξ=1)=
,p(ξ=1)=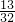 ,p(ξ=2)=
,p(ξ=2)= ,p(ξ=3)=
,p(ξ=3)=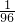 ,由此能够求出三辆客车中被堵车辆的辆数ξ的数学期望和方差.
,由此能够求出三辆客车中被堵车辆的辆数ξ的数学期望和方差.
点评:本题n次独立重复试验恰好发生k次的概率,解题时要认真审题,注意挖掘题设中的隐含条件.
 ,不堵车的概率为
,不堵车的概率为 ,
,设客车走高速公路堵车的概率是p,不堵车的概率是1-p,
∴
 ,
,解得p=
 .
.(II)ξ可能的取值是0,1,2,3,
p(ξ=0)=
 =
=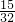 ,
,p(ξ=1)=
 ,
,p(ξ=2)=
 ,
,p(ξ=3)=
 ,
,∴Eξ=0×
 ,
,Dξ=
 +
+ .
.分析:(I)客车走一级公路堵车的概率为
 ,不堵车的概率为
,不堵车的概率为 ,设客车走高速公路堵车的概率是p,不堵车的概率是1-p,由题设知
,设客车走高速公路堵车的概率是p,不堵车的概率是1-p,由题设知 ,从而得到客车走高速公路被堵车的概率.
,从而得到客车走高速公路被堵车的概率.(II)ξ可能的取值是0,1,2,3,p(ξ=0)=
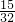 ,p(ξ=1)=
,p(ξ=1)=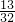 ,p(ξ=2)=
,p(ξ=2)= ,p(ξ=3)=
,p(ξ=3)=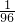 ,由此能够求出三辆客车中被堵车辆的辆数ξ的数学期望和方差.
,由此能够求出三辆客车中被堵车辆的辆数ξ的数学期望和方差.点评:本题n次独立重复试验恰好发生k次的概率,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
相关题目
 ;若1号、2号两辆客车走一级公路,3号客车走高速公路,且三辆客车是否被堵车相互之间没有影响,若三辆客车中恰有一辆被堵车的概率为
;若1号、2号两辆客车走一级公路,3号客车走高速公路,且三辆客车是否被堵车相互之间没有影响,若三辆客车中恰有一辆被堵车的概率为 .
.