题目内容
(1)证明:|a+b|+|a-b|≥2|a|,并说明等号成立的条件;
(2)若不等式|a+b|+|a-b|≥|a|(|x-2|+|x-3|)对任意的实数a(a≠0)和b恒成立,求实数x的取值范围.
(2)若不等式|a+b|+|a-b|≥|a|(|x-2|+|x-3|)对任意的实数a(a≠0)和b恒成立,求实数x的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)利用绝对值不等式的几何意义即可证得:|a+b|+|a-b|≥2|a|,并能求得等号成立的条件;
(2)由(1)得
≥2,于是|x-2|+|x-3|≤2恒成立,通过对自变量x范围的分类讨论,去掉式中的绝对值符号,再解相应的不等式,最后取并即可.
(2)由(1)得
| |a+b|+|a-b| |
| |a| |
解答:
(1)证明:|a+b|+|a-b|≥|(a+b)+(a-b)|=2|a|,…3分
当且仅当(a-b)(a+b)≥0时等号成立,即|a|≥|b|…5分
(2)解:由(1)得
≥2,即
的最小值为2,
于是|x-2|+|x-3|≤2…6分
当x<2时,原不等式化为-(x-2)-(x-3)≤2,解得x≥
,
所以x的取值范围是
≤x<2;…7分
当2≤x≤3时,原不等式化为(x-2)-(x-3)≤2,即-5≤2恒成立,
所以x的取值范围是2≤x≤3;…8分
当x>3时,原不等式化为(x-2)+(x-3)≤2,解得x≤
,
所以x的取值范围是3<x≤
;…9分
综上所述,x的取值范围是
≤x≤
…10分
当且仅当(a-b)(a+b)≥0时等号成立,即|a|≥|b|…5分
(2)解:由(1)得
| |a+b|+|a-b| |
| |a| |
| |a+b|+|a-b| |
| |a| |
于是|x-2|+|x-3|≤2…6分
当x<2时,原不等式化为-(x-2)-(x-3)≤2,解得x≥
| 3 |
| 2 |
所以x的取值范围是
| 3 |
| 2 |
当2≤x≤3时,原不等式化为(x-2)-(x-3)≤2,即-5≤2恒成立,
所以x的取值范围是2≤x≤3;…8分
当x>3时,原不等式化为(x-2)+(x-3)≤2,解得x≤
| 7 |
| 2 |
所以x的取值范围是3<x≤
| 7 |
| 2 |
综上所述,x的取值范围是
| 3 |
| 2 |
| 7 |
| 2 |
点评:本题考查绝对值不等式的解法,着重考查等价转化思想与分类讨论思想的综合应用,考查运算求解能力,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点.
如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点. 如图,△ABC内接于⊙O,AB=AC,点D在⊙O上,AD⊥AB,AD交BC于点E,点F在DA的延长线上,AF=AE,求证:
如图,△ABC内接于⊙O,AB=AC,点D在⊙O上,AD⊥AB,AD交BC于点E,点F在DA的延长线上,AF=AE,求证: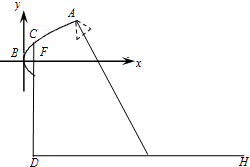 为了迎接青奥会,南京将在主干道统一安装某种新型节能路灯,该路灯由灯柱和支架组成.在如图所示的直角坐标系中,支架ACB是抛物线y2=2x的一部分,灯柱CD经过该抛物线的焦点F且与路面垂直,其中C在抛物线上,B为抛物线的顶点,DH表示道路路面,BF∥DH,A为锥形灯罩的顶,灯罩轴线与抛物线在A处的切线垂直.安装时要求锥形灯罩的顶到灯柱的距离是1.5米,灯罩的轴线正好通过道路路面的中线.
为了迎接青奥会,南京将在主干道统一安装某种新型节能路灯,该路灯由灯柱和支架组成.在如图所示的直角坐标系中,支架ACB是抛物线y2=2x的一部分,灯柱CD经过该抛物线的焦点F且与路面垂直,其中C在抛物线上,B为抛物线的顶点,DH表示道路路面,BF∥DH,A为锥形灯罩的顶,灯罩轴线与抛物线在A处的切线垂直.安装时要求锥形灯罩的顶到灯柱的距离是1.5米,灯罩的轴线正好通过道路路面的中线.