题目内容
如图,在四棱柱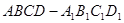 中,已知平面
中,已知平面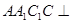 平面
平面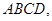 且
且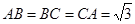 ,
,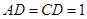 .
.
(1)求证:
(2)若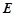 为棱
为棱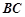 上的一点,且
上的一点,且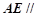 平面
平面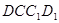 ,求线段
,求线段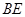 的长度
的长度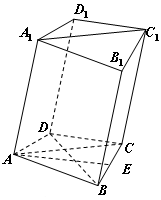
(1) 详见解析,(2) 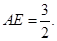
解析试题分析:(1)先根据面面垂直性质定理,将面面垂直条件转化为线面垂直:在四边形 中,因为
中,因为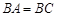 ,
,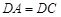 ,所以
,所以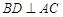 ,又平面
,又平面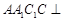 平面
平面 ,且平面
,且平面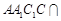 平面
平面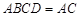 ,
,  平面
平面 ,所以
,所以 平面
平面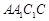 ,再利用线面垂直性质定理转化为线线垂直:因为
,再利用线面垂直性质定理转化为线线垂直:因为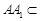 平面
平面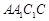 ,所以
,所以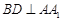 ,(2)先根据线面平行性质定理,将线面平行转化为线线平行:因为
,(2)先根据线面平行性质定理,将线面平行转化为线线平行:因为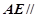 平面
平面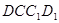 ,
,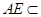 平面
平面 ,平面
,平面 平面
平面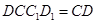 ,所以
,所以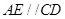 然后在平面
然后在平面 中解得
中解得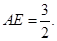
(1)四边形 中,因为
中,因为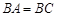 ,
,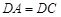 ,所以
,所以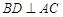 , 2分
, 2分
又平面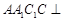 平面
平面 ,且平面
,且平面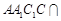 平面
平面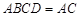 ,
,  平面
平面 ,
,
所以 平面
平面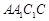 ,------5分
,------5分
又因为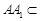 平面
平面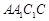 ,所以
,所以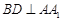 --7分
--7分
(2)因为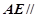 平面
平面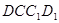 ,
,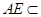 平面
平面 ,平面
,平面 平面
平面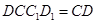 ,所以
,所以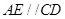 ,所以E为BC的中点,
,所以E为BC的中点,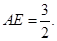 14分
14分
考点:面面垂直性质定理,线面平行性质定理

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 中,平面
中,平面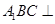 侧面
侧面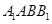 ,且
,且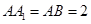
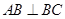 ;
;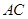 与平面
与平面 所成的角为
所成的角为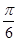 ,求锐二面角
,求锐二面角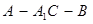 的大小。
的大小。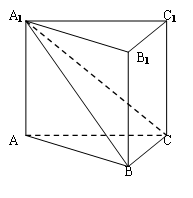

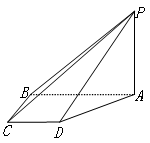
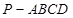 中,
中,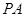 ⊥底面
⊥底面 ,四边形
,四边形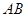 ⊥
⊥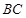 ,
,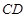 ,
,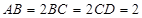 ,
,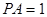 .
.
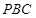 ⊥平面
⊥平面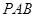 ;
;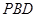 的距离;
的距离;
 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,
, ,
, 是线段
是线段 的中点.
的中点.
 ;
; 垂直于平面
垂直于平面 ,求平面
,求平面 和平面
和平面 中,
中, ,
, .将
.将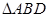 沿
沿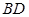 折起,使得平面
折起,使得平面
 平面
平面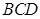 ,如图.
,如图.
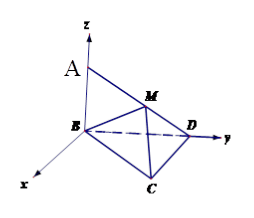
 ;
; 为
为 中点,求直线
中点,求直线 所成角的正弦值.
所成角的正弦值. 底面ABCD,侧棱
底面ABCD,侧棱 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB
 中,
中, =
= ,
,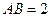 ,点
,点 为棱
为棱 的中点,则二面角
的中点,则二面角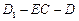 的大小为 (结果用反三角函数值表示)
的大小为 (结果用反三角函数值表示)