题目内容
抛物线y=
解析:设A(x1,y1),B(x2,y2),AB的中点M(x0,y0),
则
由点差法得![]() =
=![]() (x1+x2)=-
(x1+x2)=-![]() ,
,
即kAB=-![]() .
.
又x0=![]() =-
=-![]() ,
,
y0=![]() (x12+x22)=
(x12+x22)=![]() [(x1+x2)2-2x1x2]=
[(x1+x2)2-2x1x2]=![]() (p2-2q),
(p2-2q),
∴M(-![]() p,
p,![]() (p2-2q)).
(p2-2q)).
∴AB的方程为y-![]() (p2-2q)=-
(p2-2q)=-![]() (x+
(x+![]() p),即px+3y+q=0(p2-4q>0).
p),即px+3y+q=0(p2-4q>0).
答案:px+3y+q=0(p2-4q>0).

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
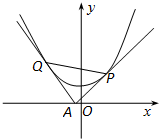 过x轴上动点A(a,0)引抛物线y=x2+1的两条切线AP、AQ,P、Q为切点.
过x轴上动点A(a,0)引抛物线y=x2+1的两条切线AP、AQ,P、Q为切点.