题目内容
集合A={a,b},B={1,2},则从集合A到集合B的映射有________个.
4
由题知;法1:A集合中两个元素,B集合中两个元素,利用映射概念可以得解.
法2:利用已知结论:若A={a1,a2.…an},B={b1,b2…bm},则A到B的映射共有mn个.
解答:法1:由映射定义可知:
A到B的映射有以下几种:(1):a→1,b→1;(2):a→2,b→2;(3)a→1,b→2;(4)a→2,b→1,
共4种.
法2:已知结论:若A={a1,a2.…an},B={b1,b2…bm},则A到B的映射共有mn个,
可知,A集合中两个元素,B集合中两个元素,
所以共有22=4种映射.
故答案为:4.
点评:本题考查映射概念,高考中主要是小题,解决本题:
(1)利用定义.
(2)利用已知结论.第二种方法需要记住结论:若A={a1,a2.…an},B={b1,b2…bm},则A到B的映射共有mn个.
由题知;法1:A集合中两个元素,B集合中两个元素,利用映射概念可以得解.
法2:利用已知结论:若A={a1,a2.…an},B={b1,b2…bm},则A到B的映射共有mn个.
解答:法1:由映射定义可知:
A到B的映射有以下几种:(1):a→1,b→1;(2):a→2,b→2;(3)a→1,b→2;(4)a→2,b→1,
共4种.
法2:已知结论:若A={a1,a2.…an},B={b1,b2…bm},则A到B的映射共有mn个,
可知,A集合中两个元素,B集合中两个元素,
所以共有22=4种映射.
故答案为:4.
点评:本题考查映射概念,高考中主要是小题,解决本题:
(1)利用定义.
(2)利用已知结论.第二种方法需要记住结论:若A={a1,a2.…an},B={b1,b2…bm},则A到B的映射共有mn个.

练习册系列答案
相关题目
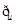 B)=R,则实数a的取值范围是 ( )
B)=R,则实数a的取值范围是 ( )