Question

椭圆C的焦点在x轴上，焦距为2，直线n：x-y-1=0与椭圆C交于A、B两点，F₁是左焦点，且F₁A⊥F₁B，则椭圆C的标准方程是

 

．

Answer 1

分析：根据题意算出c=1，从而设椭圆C的方程为

x2

m

+

y2

m-1

=1（m＞1），与直线n的方程联解消去y可得（2m-1）x²-2mx+2m-m²=0．设A（x₁，y₁），B（x₂，y₂），由F₁A⊥F₁B，利用向量数量积的运算性质得出

F1A

•

F1B

=0，根据坐标运算化简可得x₁x₂+1=0，由根与系数的关系建立关于m的方程，解出m的值即可得到椭圆C的标准方程．

解答：解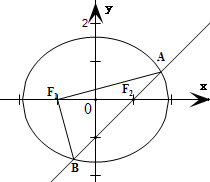：∵椭圆C的焦点在x轴上，焦距为2，
∴c=1，椭圆的焦点为F₁（-1，0）与F₂（1，0），
设椭圆C的方程为

x2

m

+

y2

m-1

=1（m＞1），
由

x-y-1=0 x2 m + y2 m-1 =1

消去y，得（2m-1）x²-2mx+2m-m²=0．
设A（x₁，y₁），B（x₂，y₂），可得x₁+x₂=

2m

2m-1

，x₁x₂=

2m-m2

2m-1

．
∵

F1A

=（x₁+1，y₁），

F1B

=（x₂+1，y₂），F₁A⊥F₁B，
∴

F1A

•

F1B

=0，即（x₁+1）（x₂+1）+y₁y₂=0，
可得（x₁+1）（x₂+1）+（x₁-1）（x₂-1）=0，
化简得x₁x₂+1=0，即

2m-m2

2m-1

=-1，解得m=2±

3

．
由于m＞1，
∴m=2-

3

不符合题意，可得m=2+

3

．
∴椭圆C的标准方程是

x2

2+ 3

+

y2

1+ 3

=1．
故答案为：

x2

2+ 3

+

y2

1+ 3

=1

点评：本题给出椭圆满足的条件，求椭圆的标准方程．着重考查了椭圆的标准方程与简单几何性质、直线与圆锥曲线的位置关系等知识，属于中档题．