题目内容
已知多面体ABC-DEFG,AB,AC,AD两两垂直,面ABC//面DEFG,面BEF//面ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为( )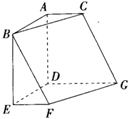
| A.2 | B.4 | C.6 | D.8 |
B
解析试题分析:取CD中点H,连接AH,FH,则原多面体分割成棱柱BEF-ADH和棱柱ABC-HFG,两棱柱体积分别为2和2,所以原几何体体积为4
考点:几何体体积
点评:将原几何体分割成两个棱柱,分别求其体积

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图是一个几何体的正视图和侧视图。其俯视图是面积为 的矩形。则该几何体的体积是
的矩形。则该几何体的体积是
| A.8 | B. |
| C.16 | D. |
已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题:
①若m⊥α,m⊥β,则α∥β;
②若α⊥γ,β⊥α,则α∥β;
③若m∥α,n∥β,m∥n,则α∥β;
④若m、n是异面直线,m⊥α,m∥β,n⊥β,n∥α,则α⊥β
其中真命题是( )
| A.①和② | B.①和③ | C.③和④ | D.①和④ |
如图,三棱柱A1B1C1—ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( ).
| A.AE、B1C1为异面直线,且AE⊥B1C1 |
| B.AC⊥平面A1B1BA |
| C.CC1与B1E是异面直线 |
| D.A1C1∥平面AB1E |
已知a、b是异面直线,直线c//a,那么c与b ( )
| A.一定是异面直线 | B.一定是相交直线 |
| C.不可能是相交直线 | D.不可能是平行直线 |
( )如图,正四棱锥 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是
A. | B. | C. | D. |
下列说法不正确的是( )
| A.空间中,一组对边平行且相等的四边形是一定是平行四边形; |
| B.过一条直线有且只有一个平面与已知平面垂直. |
| C.过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内; |
D.存在两条异面直线 ,使得 ,使得 ; ; |


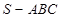 的所有顶点都在球O的表面上,三角形ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为( )
的所有顶点都在球O的表面上,三角形ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为( )


