题目内容
已知数列{an}的前n项和Sn=an2+bn+c(n∈N*),且S1=3,S2=7,S3=13,
(1)求数列{an}的通项公式;
(2)求数列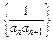 的前n项和Tn.
的前n项和Tn.
(1)求数列{an}的通项公式;
(2)求数列
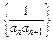 的前n项和Tn.
的前n项和Tn.(1)an= (2)Tn=
(2)Tn=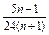 (n∈N*)
(n∈N*)
 (2)Tn=
(2)Tn=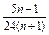 (n∈N*)
(n∈N*)(1)由已知有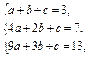 解得
解得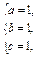
所以Sn=n2+n+1.
当n≥2时,
an=Sn-Sn-1=n2+n+1-[(n-1)2+(n-1)+1]=2n,
所以an=
(2)令bn=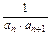 ,则b1=
,则b1=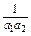 =
=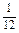 .
.
当n≥2时,bn=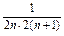 =
= ·
·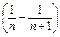 .
.
所以b2+…+bn
=
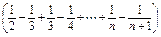
=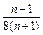 .所以Tn=
.所以Tn=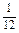 +
+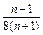 =
=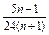 (n∈N*).
(n∈N*).
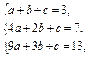 解得
解得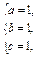
所以Sn=n2+n+1.
当n≥2时,
an=Sn-Sn-1=n2+n+1-[(n-1)2+(n-1)+1]=2n,
所以an=

(2)令bn=
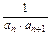 ,则b1=
,则b1=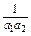 =
=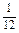 .
.当n≥2时,bn=
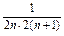 =
= ·
·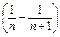 .
.所以b2+…+bn
=

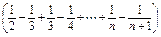
=
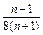 .所以Tn=
.所以Tn=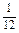 +
+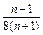 =
=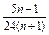 (n∈N*).
(n∈N*).
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 时,求Sn.
时,求Sn.

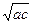
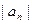 满足:
满足: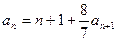 ,且存在大于1的整数k使
,且存在大于1的整数k使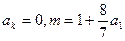 。
。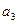 表示m(不必化简)
表示m(不必化简)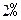 并按复利计算,问每年应该存入多少钱?
并按复利计算,问每年应该存入多少钱?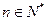 ,点(n,Sn)总在抛物线y=ax2+bx+c
,点(n,Sn)总在抛物线y=ax2+bx+c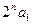 +
+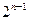 a2+
a2+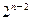 a3+…+
a3+…+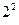
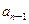 +2
+2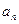 .
.