题目内容
10.已知函数f(x)=xsinx+cosx(x>0).(1)当x∈(0,2π)时,求f(x)的极值;
(2)记xi为f(x)的从小到大的第i(i∈N*)个极值点,证明:$\frac{1}{{{x}_{2}}^{2}}$+$\frac{1}{{{x}_{3}}^{2}}$+…+$\frac{1}{{{x}_{n}}^{2}}$<$\frac{2}{9}$(n≥2,n∈N)
分析 (1)求导数,确定函数的单调性,即可求f(x)的极值;
(2)确定xi=$\frac{(2n-1)π}{2}$,可得$\frac{9}{4}×\frac{1}{{{x}_{i}}^{2}}$=$[\frac{3}{(2n-1)π}]^{2}$<$\frac{1}{(2n-1)^{2}}$,利用裂项法,即可证明结论.
解答 解:(1)∵f(x)=xsinx+cosx,
∴f′(x)=sinx+xcosx-sinx=xcosx,x∈(0,2π),
f′(x)=0,∴x=$\frac{π}{2}$或$\frac{3π}{2}$
∴f(x) 在(0,$\frac{π}{2}$),($\frac{3π}{2}$,2π)递增,($\frac{π}{2}$,$\frac{3π}{2}$)递减,…(2分)
∴f(x)极小值=-$\frac{3π}{2}$,f(x)极大值=$\frac{π}{2}$;…(6分)
(Ⅱ)∵f′(x)=0,x>0,∴xi=$\frac{(2n-1)π}{2}$,…(8分)
∴$\frac{9}{4}×\frac{1}{{{x}_{i}}^{2}}$=$[\frac{3}{(2n-1)π}]^{2}$<$\frac{1}{(2n-1)^{2}}$,…(9分)
∴$\frac{9}{4}$($\frac{1}{{{x}_{2}}^{2}}$+$\frac{1}{{{x}_{3}}^{2}}$+…+$\frac{1}{{{x}_{n}}^{2}}$)<$\frac{1}{{3}^{2}}$+$\frac{1}{{5}^{2}}$+…+$\frac{1}{(2n-1)^{2}}$
<$\frac{1}{1×3}$+$\frac{1}{3×5}$+…+$\frac{1}{(2n-3)(2n-1)}$=$\frac{1}{2}$(1-$\frac{1}{2n-1}$)=$\frac{1}{2}$-$\frac{1}{4n-2}$<$\frac{1}{2}$,
∴$\frac{1}{{{x}_{2}}^{2}}$+$\frac{1}{{{x}_{3}}^{2}}$+…+$\frac{1}{{{x}_{n}}^{2}}$<$\frac{2}{9}$(n≥2,n∈N).…(12分)
点评 本题考查导数知识的运用,考查不等式的证明,考查放缩法的运用,属于中档题.

| A. | 若直线l∥平面α,直线l∥平面β,则α∥β. | |
| B. | 若直线l⊥平面α,直线l⊥平面β,则α∥β. | |
| C. | 若直线l1,l2与平面α所成的角相等,则l1∥l2 | |
| D. | 若直线l上两个不同的点A,B到平面α的距离相等,则l∥α |
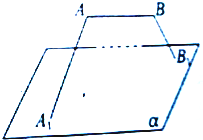 线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=2,A1B1=4,求AB与平面α的距离.
线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=2,A1B1=4,求AB与平面α的距离.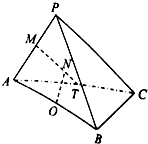 如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.
如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.