题目内容
(1)已知数列{an}的前n项和Sn=2an+1,求{an}的通项公式.(2)已知等比数列{an}中,
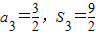 ,求{an}的通项公式.
,求{an}的通项公式.
【答案】分析:(1)由题意n=1时,可求a1,然后n≥2时,Sn=2an+1,Sn-1=2an-1+1,两式相减可得数列的项之间的递推公式,结合等比数列的通项公式即可求解
(2)当公比q=1时,S3=3a3满足题意,当q≠1时,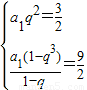 两式相除可求公比q及首项a1,从而可求
两式相除可求公比q及首项a1,从而可求
解答:解:(1)∵Sn=2an+1
当n=1时,有S1=2a1+1即a1=-1
当n≥时,Sn=2an+1,Sn-1=2an-1+1,两式相减可得Sn-Sn-1=2an-2an-1
即an=2an-1
∴{an}是以-1为首项,以2为公比的等比数列
∴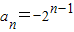
(2)当公比q=1时,S3=3a3满足题意,此时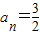
当q≠1时,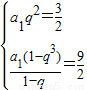 两式相除可得
两式相除可得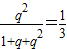
∴2q2-q-1=0
∴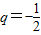 ,a1=6
,a1=6
∴an=6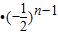
综上可得,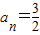 或an=6
或an=6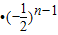
点评:本题主要考查了利用数列的和之间的递推公式求解数列的通项公式,等比数列的通项公式及求和公式的简单应用.
(2)当公比q=1时,S3=3a3满足题意,当q≠1时,
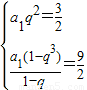 两式相除可求公比q及首项a1,从而可求
两式相除可求公比q及首项a1,从而可求解答:解:(1)∵Sn=2an+1
当n=1时,有S1=2a1+1即a1=-1
当n≥时,Sn=2an+1,Sn-1=2an-1+1,两式相减可得Sn-Sn-1=2an-2an-1
即an=2an-1
∴{an}是以-1为首项,以2为公比的等比数列
∴
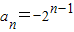
(2)当公比q=1时,S3=3a3满足题意,此时
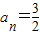
当q≠1时,
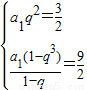 两式相除可得
两式相除可得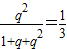
∴2q2-q-1=0
∴
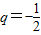 ,a1=6
,a1=6∴an=6
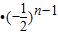
综上可得,
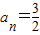 或an=6
或an=6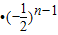
点评:本题主要考查了利用数列的和之间的递推公式求解数列的通项公式,等比数列的通项公式及求和公式的简单应用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
(1)已知数列{an}的第1项 a1=1,且an+1=
( n=1,2,3…)使用归纳法归纳出这个数列的通项公式.(不需证明)
(2)用分析法证明:若a>0,则
-
≥a+
-2.
| an |
| 1+an |
(2)用分析法证明:若a>0,则
a2+
|
| 2 |
| 1 |
| a |