题目内容
P是平行四边形ABCD外的一点,Q是PA的中点,求证:PC∥平面BDQ.
证明见解析
解析:
证明:如图,连结AC交BD于O
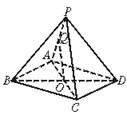
∵ ABCD是平行四边形,
∴ AO=OC
连结OQ,则OQ![]() 平面BDQ,
平面BDQ,
且OQ是△APC的中位线
∴ PC∥OQ,又PC在平面BDQ外
∴ PC∥平面BDQ.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
题目内容
P是平行四边形ABCD外的一点,Q是PA的中点,求证:PC∥平面BDQ.
证明见解析
证明:如图,连结AC交BD于O

∵ ABCD是平行四边形,
∴ AO=OC
连结OQ,则OQ![]() 平面BDQ,
平面BDQ,
且OQ是△APC的中位线
∴ PC∥OQ,又PC在平面BDQ外
∴ PC∥平面BDQ.

 智慧小复习系列答案
智慧小复习系列答案