题目内容
(本小题满分14分)
已知函数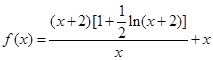
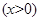
(1)设 在
在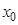 处取得极值,且
处取得极值,且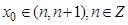 ,求
,求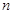 的值,并说明
的值,并说明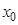 是极大值点还是极小值点;
是极大值点还是极小值点;
(2)求证: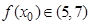
(1)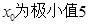 ;(2))
;(2))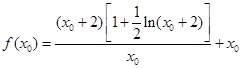
∴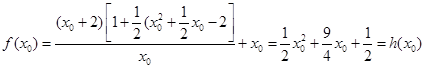
其中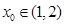 中
中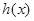 单调递增
单调递增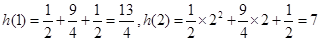
又∵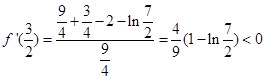 由二分法知:
由二分法知: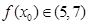
解析试题分析:(1)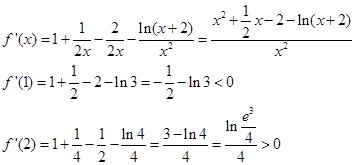
∴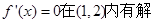
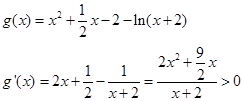
∴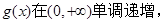 ∴
∴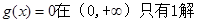
∴ 即
即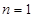
又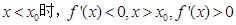 ∴
∴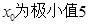
(2)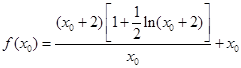
又∵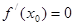 ∴
∴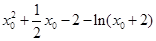 得:
得: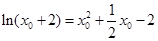
∴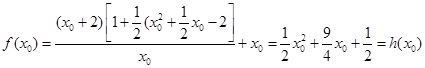
其中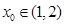 中
中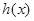 单调递增
单调递增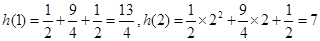
又∵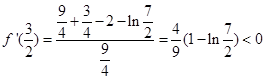 由二分法知:
由二分法知: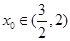
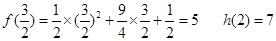 ∴
∴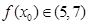
考点:利用导数研究函数的单调性;利用导数研究函数的极值;导数的综合应用;二分法。
点评:此题主要考查函数在某点取得极值的条件:极值点的导数为0,但导数为0的点不一定是极值点。考查的知识点比较全面,综合性比较强,是一道中档题,也是高考的热点问题。

练习册系列答案
相关题目
 ,
,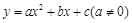 ,
,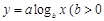 且
且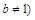 ,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量. 是定义在
是定义在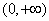 上的单调增函数,满足
上的单调增函数,满足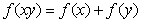 ,
,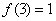 ;
;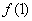 ;
; 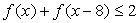 ,求
,求 的取值范围。
的取值范围。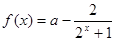 ,其中
,其中 为常数
为常数 为奇函数,试确定
为奇函数,试确定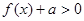 恒成立,求实数
恒成立,求实数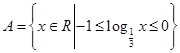 ,函数
,函数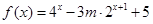 (其中
(其中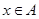 ,
, )
)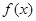 的定义域;
的定义域;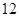 分)已知函数
分)已知函数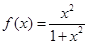 .
.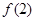 与
与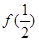 ,
,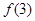 与
与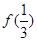 ;
; 与
与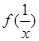 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;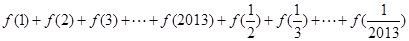 的值 .
的值 . 为定义在
为定义在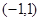 上的奇函数,当
上的奇函数,当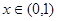 时,
时,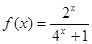 ;
;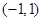 上的解析式;
上的解析式;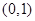 上的单调性,并给出证明.
上的单调性,并给出证明.