题目内容

已知Q（2，1），F为抛物线y2=4x的焦点，P是抛物线上一个动点，则|PF|+|PQ|的最小值为
3
3
．
分析：利用抛物线的定义和三角形三边大小关系及三点共线的性质即可得出．
解答：解：由抛物线y2=4x得
p
2
=
4
4
=1，得准线l方程为x=-1．
过点Q作QM⊥准线l，M为垂足，则|PF|=|PM|．
当直线PQ∥x轴时，则|PF|+|PQ|取得最小值|QM|，
则|PF|+|PQ|的最小值=|QM|=2-（-1）=3．
故答案为3．
点评：熟练掌握抛物线的定义和三角形三边大小关系是解题的关键．
练习册系列答案
相关题目
（1）在一个红绿灯路口，红灯、黄灯和绿灯的时间分别为30秒、5秒和40秒．当你到达路口时，求不是红灯的概率．
（2）已知关于x的一元二次函数f（x）=ax2-4bx+1．设集合P={1，2，3}和Q={-1，1，2，3，4}，分别从集合P和Q中随机取一个数作为a和b，求函数y=f（x）在区间[1，+∞）上是增函数的概率．
已知定点A(0，
3
)，点B在圆F：x2+(y-
3
)2=16上运动，F为圆心，线段AB的垂直平分线交BF于点P．
（1）求动点P的轨迹E的方程；
（2）若曲线Q：x2-2ax+y2+a2=
1
4
被轨迹E包围着，求实数a的最小值；
（3）已知Q（2，0），求|PQ|的最大值．
已知关于x的二次函数f(x)=ax2-2bx+1，
（1）已知集合P={-2，1，2 }，Q={-1，1，2}，分别从集合P和Q中随机取一个数作为a和b，求函数y=f(x)在区间[1，+∞)上是增函数的概率；
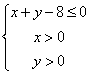（2）在区域内随机任取一点(a，b)，求函数y=f(x)在区间[1，+∞)上是增函数的概率。

已知定点A，点B在圆F：上运动，F为圆心，线段AB的垂直平分线交BF于点P .

(1)求动点P的轨迹E的方程；

(2)若曲线Q：被轨迹E包围着，求实数的最小值；

(3)已知Q（2，0），求︱PQ︱的最大值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网