题目内容
已知关于x的二次函数f(x)=ax2-2bx+1,
(1)已知集合P={-2,1,2 },Q={-1,1,2},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率;
(2)在区域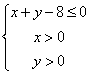 内随机任取一点(a,b),求函数y=f(x)在区间[1,+∞)上是增函数的概率。
内随机任取一点(a,b),求函数y=f(x)在区间[1,+∞)上是增函数的概率。
(1)已知集合P={-2,1,2 },Q={-1,1,2},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率;
(2)在区域
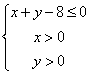 内随机任取一点(a,b),求函数y=f(x)在区间[1,+∞)上是增函数的概率。
内随机任取一点(a,b),求函数y=f(x)在区间[1,+∞)上是增函数的概率。 解:(1)要使函数f(x)=ax2-2bx+1在区间[1,+∞)上是增函数,须有对称轴 且a>0,
且a>0,
分别从集合P和Q中随机取一个数作为a和b,有(-2,-1),(-2,1),(-2,2),(1,-1),
(1,1),(1,2),(2,-1),(2,1),(2,2)共9个,
其中符合要求的有(1,-1),(1,1),(1,2)(2,-1),(2,2)共5个,
设“能使函数函数y=f(x)在区间[1,+∞)上是增函数的事件为A,则P(A)= 。
。
(2)设“在区域内任限一个点(a,b),能使函数函数y=f(x)在区间[1,+∞)上是增函数的事件为B,则P(B)= 。
。
 且a>0,
且a>0,分别从集合P和Q中随机取一个数作为a和b,有(-2,-1),(-2,1),(-2,2),(1,-1),
(1,1),(1,2),(2,-1),(2,1),(2,2)共9个,
其中符合要求的有(1,-1),(1,1),(1,2)(2,-1),(2,2)共5个,
设“能使函数函数y=f(x)在区间[1,+∞)上是增函数的事件为A,则P(A)=
 。
。 (2)设“在区域内任限一个点(a,b),能使函数函数y=f(x)在区间[1,+∞)上是增函数的事件为B,则P(B)=
 。
。
练习册系列答案
相关题目
 已知关于x的二次函数f(x)=x2+ax-b(a,b∈R).
已知关于x的二次函数f(x)=x2+ax-b(a,b∈R).