题目内容
设ABCD是半径为2的球面上四个不同的点，且满足
•
=0，
•
=0，
•
=0，则S△ABC+S△ABD+S△ACD的最大值为（ ）
| AB |
| AC |
| AD |
| AC |
| AB |
| AD |
| A、16 | B、8 | C、4 | D、2 |
分析：由题意可知，三棱锥的顶点的三条直线AB，AC，AD两两垂直，可以扩展为长方体，对角线为球的直径，设出三度，表示出面积关系式，然后利用基本不等式，求出最大值．
解答：解：设AB=a，AC=b，AD=c，
因为AB，AC，AD两两互相垂直，
扩展为长方体，它的对角线为球的直径，所以a2+b2+c2=4R2=16
S△ABC+S△ACD+S△ADB
=
（ab+ac+bc ）
≤
（a2+b2+c2）=8
即最大值为：8
故选B
因为AB，AC，AD两两互相垂直，
扩展为长方体，它的对角线为球的直径，所以a2+b2+c2=4R2=16
S△ABC+S△ACD+S△ADB
=
| 1 |
| 2 |
≤
| 1 |
| 2 |
即最大值为：8
故选B
点评：本题是基础题，考查球的内接多面体，基本不等式求最值问题，能够把几何体扩展为长方体，推知多面体的外接球是同一个球，是解题的关键．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
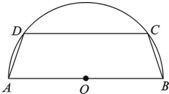有一块半径为2的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O的直径，上底CD的端点在圆周上．
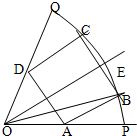如图，已知OPQ是半径为1，圆心角为60°的扇形，∠POQ的平分线交弧PQ于点E，扇形POQ的内接矩形ABCD关于OE对称；设∠POB=α，矩形ABCD的面积为S．
•
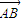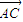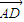=0，
•
=0，
•
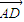=0，则S△ABC+S△ABD+S△ACD的最大值为（ ）