题目内容
椭圆焦点在x轴上,A为该椭圆右顶点,P在椭圆上一点,∠OPA=90°,则该椭圆的离心率e的范围是( )
A、[
| ||||||
B、(
| ||||||
C、[
| ||||||
D、(0,
|
分析:可设椭圆的标准方程为:
+
=1(a>b>0).设P(x,y),由于∠OPA=90°,可得点P在以OA为直径的圆上.该圆为:(x-
)2+y2=(
)2,化为x2-ax+y2=0.与椭圆的方程联立可得:(b2-a2)x2+a3x-a2b2=0,得到ax=
,解得x=
,由于0<x<a,可得0<
<a,解出即可.
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| 2 |
| a |
| 2 |
| -a2b2 |
| b2-a2 |
| ab2 |
| c2 |
| ab2 |
| c2 |
解答:解:可设椭圆的标准方程为:
+
=1(a>b>0).
设P(x,y),∵∠OPA=90°,∴点P在以OA为直径的圆上.
该圆为:(x-
)2+y2=(
)2,化为x2-ax+y2=0.
联立
化为(b2-a2)x2+a3x-a2b2=0,
则ax=
,解得x=
,
∵0<x<a,∴0<
<a,
化为c2>b2=a2-c2,
∴e2>
,又1>e>0.
解得
<e<1.
∴该椭圆的离心率e的范围是(
,1).
故选:C.
| x2 |
| a2 |
| y2 |
| b2 |
设P(x,y),∵∠OPA=90°,∴点P在以OA为直径的圆上.
该圆为:(x-
| a |
| 2 |
| a |
| 2 |
联立
|
则ax=
| -a2b2 |
| b2-a2 |
| ab2 |
| c2 |
∵0<x<a,∴0<
| ab2 |
| c2 |
化为c2>b2=a2-c2,
∴e2>
| 1 |
| 2 |
解得
| ||
| 2 |
∴该椭圆的离心率e的范围是(
| ||
| 2 |
故选:C.
点评:本题考查了椭圆与圆的标准方程及其性质,考查了分析问题和解决问题的能力,属于难题.

练习册系列答案
相关题目
 ,则该椭圆的离心率e的范围是(
)
,则该椭圆的离心率e的范围是(
)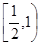 B.
B.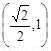 C.
C.  D.
D.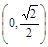
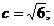
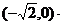
 C.
C.  D.
D.