题目内容
椭圆焦点在x轴上,A为该椭圆右顶点,P在椭圆上一点, ,则该椭圆的离心率e的范围是(
)
,则该椭圆的离心率e的范围是(
)
A.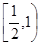 B.
B.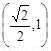 C.
C.  D.
D.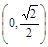
【答案】
B
【解析】
试题分析:设 则
则 .又由于
.又由于 ,所以
,所以 即可得
即可得 .所以点P在以OA为直径的圆上.及椭圆与该圆有公共点.
.所以点P在以OA为直径的圆上.及椭圆与该圆有公共点.  消去y得
消去y得 .由于过点A所以有一个根为
.由于过点A所以有一个根为 ,另一个根设为
,另一个根设为 ,则由韦达定理可得
,则由韦达定理可得 .又因为
.又因为 .所以解得
.所以解得 .故选B.
.故选B.
考点:1.线的垂直问题转化到向量垂直问题.2.曲线的公共点转化为方程组的解得问题.3.区间根的问题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
椭圆焦点在x轴上,A为该椭圆右顶点,P在椭圆上一点,∠OPA=90°,则该椭圆的离心率e的范围是( )
A、[
| ||||||
B、(
| ||||||
C、[
| ||||||
D、(0,
|
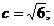
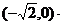
 C.
C.  D.
D.