题目内容
(本题满分12分)在斜三角形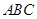 中,内角
中,内角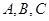 的对边分别为
的对边分别为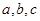 。若
。若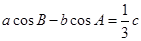 。(1)证明:
。(1)证明: ;(2)求
;(2)求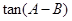 的最大值。
的最大值。
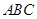 中,内角
中,内角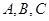 的对边分别为
的对边分别为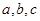 。若
。若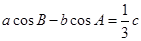 。(1)证明:
。(1)证明: ;(2)求
;(2)求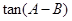 的最大值。
的最大值。(1)见解析;(2)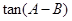 的最大值为
的最大值为 。
。
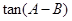 的最大值为
的最大值为 。
。试题分析:本题考查正弦定理、两角和与两角差的三角函数公式、内角和定理以及运用均值不等式求函数的最值。
(1)由
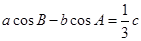 和正弦定理得
和正弦定理得 (1分)。
(1分)。又因为
 (2分),
(2分),故
 (3分),
(3分),于是
 (4分),
(4分),故
 (5分)。
(5分)。由于
 都不是直角,故
都不是直角,故 ,两边除以
,两边除以 得
得 (6分)。
(6分)。(2)由(1):
 ,故
,故 (7分)
(7分) (8分)。
(8分)。再由
 知
知 (9分),
(9分),故
 (10分)。
(10分)。因
 (11分),
(11分),故
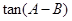 的最大值为
的最大值为 (12分)。
(12分)。点评:综合性较强,不但对正弦定理、两角和与差的三角函数进行了考查,而且考查了均值定理的应用。应用均值定理,应遵循“一正、二定、三相等”的方法要求,其中“三相等”最易被忽视。

练习册系列答案
相关题目
 中,
中, ,
, ,
, 分别是三内角A,B,C所对的三边,已知
分别是三内角A,B,C所对的三边,已知 .
. ,试判断
,试判断 ,
, ,
, 且
且 ,
, 的值;
的值; 三内角
三内角 所对边分别为
所对边分别为 且
且 ,求
,求 在
在 上的值域.
上的值域.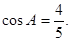
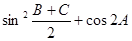 的值;(2)若
的值;(2)若 的值。
的值。 ,点D 在BC边上,∠ADC=45°。
,点D 在BC边上,∠ADC=45°。 的大小;(2)求AD的长。
的大小;(2)求AD的长。
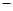 c)cosA=acosC,则角A=
c)cosA=acosC,则角A= 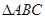 ,内角
,内角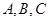 所对的边分别为
所对的边分别为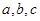 ,且满足下列三个条件:①
,且满足下列三个条件:①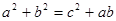 ②
②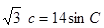 ③
③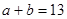
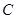 和边长
和边长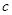 的大小; (2)
的大小; (2)  的值为____ ________。
的值为____ ________。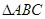 ,角
,角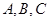 所对应的边为
所对应的边为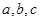 .
.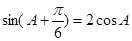 ,求
,求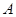 的值;
的值;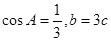 ,求
,求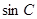 的值.
的值.