题目内容
已知数列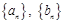 ,其中
,其中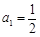 ,数列
,数列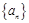 的前
的前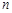 项和
项和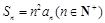 ,数列
,数列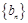 满足
满足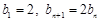 .
.
(1)求数列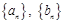 的通项公式;
的通项公式;
(2)是否存在自然数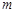 ,使得对于任意
,使得对于任意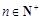 ,
,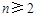 ,有
,有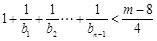 恒成立?若存在,求出
恒成立?若存在,求出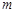 的最小值;
的最小值;
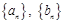 ,其中
,其中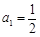 ,数列
,数列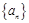 的前
的前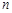 项和
项和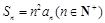 ,数列
,数列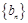 满足
满足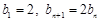 .
.(1)求数列
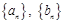 的通项公式;
的通项公式; (2)是否存在自然数
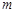 ,使得对于任意
,使得对于任意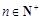 ,
,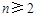 ,有
,有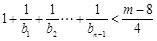 恒成立?若存在,求出
恒成立?若存在,求出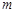 的最小值;
的最小值;(1)因为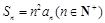 .
.
当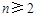 时,
时,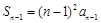 ;
;
所以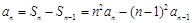 .
.
所以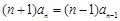 .即
.即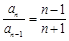 .
.
又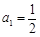 ,
,
所以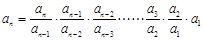
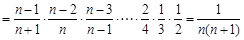 .
.
当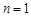 时,上式成立.
时,上式成立.
因为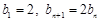 ,
,
所以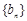 是首项为
是首项为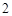 ,公比为
,公比为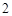 的等比数列,故
的等比数列,故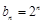 ; ----- 6分
; ----- 6分
(2)由⑴知,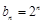 .
.
则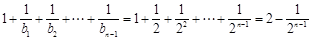 ,
,
假设存在自然数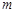 ,使得对于任意
,使得对于任意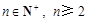 ,有
,有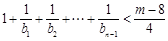 恒成立,
恒成立,
即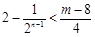 恒成立,由
恒成立,由 ,解得
,解得 ,
,
所以存在自然数
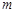 ,使得对于任意
,使得对于任意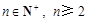 ,
,
有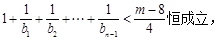 此时,
此时,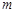 的最小值为16.
的最小值为16.
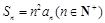 .
.当
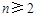 时,
时,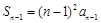 ;
;所以
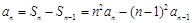 .
.所以
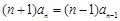 .即
.即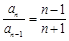 .
.又
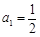 ,
,所以
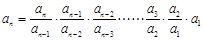
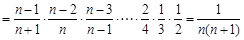 .
.当
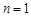 时,上式成立.
时,上式成立.因为
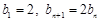 ,
,所以
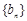 是首项为
是首项为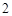 ,公比为
,公比为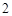 的等比数列,故
的等比数列,故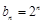 ; ----- 6分
; ----- 6分(2)由⑴知,
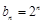 .
.则
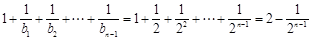 ,
,假设存在自然数
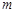 ,使得对于任意
,使得对于任意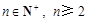 ,有
,有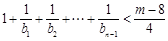 恒成立,
恒成立,即
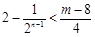 恒成立,由
恒成立,由 ,解得
,解得 ,
,所以存在自然数

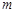 ,使得对于任意
,使得对于任意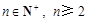 ,
,有
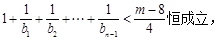 此时,
此时,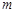 的最小值为16.
的最小值为16.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
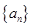 的前
的前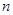 项和为
项和为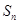 ,已知
,已知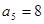 ,
,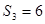 ,则
,则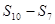 的值是 ( )
的值是 ( )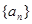 是等差数列,若
是等差数列,若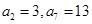 ,则数列{an}前8项的和为( )
,则数列{an}前8项的和为( )
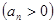 是等比数列,那么
是等比数列,那么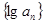 必为等差数列”,类比这个结论,可猜想:如果数列
必为等差数列”,类比这个结论,可猜想:如果数列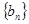 是等差数列,那么
是等差数列,那么 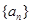 的前n项和为
的前n项和为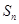 ,已知
,已知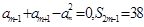
 ,则m等于
,则m等于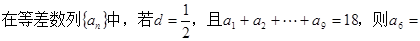
 中,若
中,若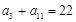 ,则
,则
 的前
的前 项和
项和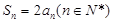 ,则下列判断中正确的是
,则下列判断中正确的是