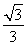题目内容
已知等差数列{an}满足：an＋1>an(n∈N*)，a1＝1，该数列的前三项分别加上1，1，3后顺次成为等比数列{bn}的前三项．
(1)分别求数列{an}、{bn}的通项公式；
(2)设Tn＝
(n∈N*)，若Tn＋
<c(c∈Z)恒成立，求c的最小值．
（1）2n（2）c＝3
【解析】(1)设d、q分别为等差数列{an}、等比数列{bn}的公差与公比，且d>0.
由a1＝1，a2＝1＋d，a3＝1＋2d，分别加上1，1，3有b1＝2，b2＝2＋d，b3＝4＋2d.
(2＋d)2＝2(4＋2d)，d2＝4.∵d>0，∴d＝2，q＝
＝2，
∴an＝1＋(n－1)×2＝2n－1，bn＝2×2n－1＝2n.
(2)Tn＝
＝
，①
Tn＝
.②
①－②，得
Tn＝
＋
，
∴Tn＝1＋
＝3－
.
∴Tn＋
－
＝3－
<3.
∵3－在N*上是单调递增的，∴3－∈[2，3)．
∴满足条件Tn＋－<c(c∈Z)恒成立的最小整数值为c＝3
练习册系列答案
全优点练单元计划系列答案
相关题目
