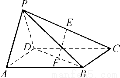
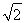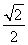题目内容
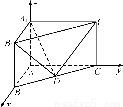
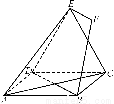
在三棱锥SABC中，SA⊥平面ABC，SA＝AB＝AC＝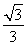
BC，点D是BC边的中点，点E是线段AD上一点，且AE＝3DE，点M是线段SD上一点，
(1)求证：BC⊥AM；
(2)若AM⊥平面SBC，求证：EM∥平面ABS.
（1）见解析（2）见解析
【解析】(1)∵AB＝AC，D是BC的中点，
∴AD⊥BC，
BC⊥AM.
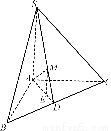
(2)∵AM⊥平面SBC，AM⊥SD，设SA＝AB＝AC＝1，则BC＝
，SD＝
，∵SA⊥AD，AM⊥SD，AD2＝MD·SD，故MD＝
，SM＝
，即SM＝3MD，又AE＝3DE，∴ME∥SA，又ME
平面ABS，SA
平面，故EM∥平面ABS.
练习册系列答案
相关题目
