题目内容
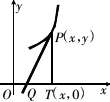
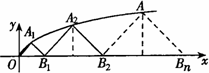
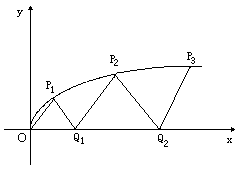
如图,曲线y2=x(y≥0)上的点Pi与x轴的正半轴上的点Qi及原点O构成一系列正三角形:△OP1Q1,△Q1P2Q2,…,△Qn-1PnQn,….设正三角形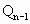 PnQn的边长为an,n∈N*(记Q0为O),Qn(Sn,0).
PnQn的边长为an,n∈N*(记Q0为O),Qn(Sn,0).
(1)求a1的值;
(2)求数列{an}的通项公式an;
(3)求证:当n≥2时,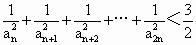 .
.
答案:
解析:
解析:
|
解 (1)由条件可得P1(
(2)∵Sn=a1+a2+…+an, ∴点Pn+1(Sn+ Sn= 于是当n≥2,n∈N*时,an=Sn-Sn-1=( 即 ∵an+1>an>0,∴an+1-an= 又当n=1时,S1= ∴a2-a1= 所以数列{an}是首项为 (3)由(2)得an=
欲证 设f(n)=4n2-7n-3,当n≥ 所以只需验证n=2时不等式成立.事实上, 综上所述,原不等式成立. |

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 a1,
a1, a1),代入曲线y2=x(y≥0),得
a1),代入曲线y2=x(y≥0),得 =
= a1.∵a1>0,∴a1=
a1.∵a1>0,∴a1= .
. an+1,
an+1, -
- -
- -
- (an+1+an)=
(an+1+an)= (an+1+an)·(an+1-an).
(an+1+an)·(an+1-an). (n≥2,n∈N*).
(n≥2,n∈N*). -
- (-
(- ,故an+1-an=
,故an+1-an=

 ,只需证3n+3<4n2-4n,即证4n2-7n-3>0.
,只需证3n+3<4n2-4n,即证4n2-7n-3>0. 时,f(n)递增.而当n≥3时,有f(n)>0成立.
时,f(n)递增.而当n≥3时,有f(n)>0成立. .
.