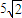Question

若动点P₁（x₁，y₁），P₂（x₂，y₂）分别在直线l₁：x-y-5=0，l₂：x-y-15=0上移动，则P₁P₂的中点P到原点的距离的最小值是（　　）

• A．

  5 2

  2

• B．5

  2

• C．

  15 2

  2

• D．15

  2

Answer 1

分析：先求得中点P所在的直线方程为 x-y-10=0，则P₁P₂的中点P到原点的距离的最小值是原点O到直线x-y-10=0的距离，利用点到直线的距离公式求得结果．

解答：解：由于点P₁（x₁，y₁），P₂（x₂，y₂）分别在2条平行直线l₁：x-y-5=0，l₂：x-y-15=0上移动，
故P₁P₂的中点P所在的直线方程为 x-y-10=0，则P₁P₂的中点P到原点的距离的最小值是原点O到直线x-y-10=0的距离，
等于

|0-0-10|

2

=5

2

，
故选B．

点评：本题主要考查两条平行线间的距离公式、点到直线的距离公式的应用，属于中档题．