��Ŀ����
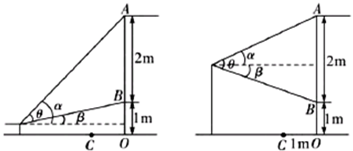 ���쳤���ڼ�С��ȥ�ιۻ�չ��Ϊ�˱����ڻ����ٰ췽�ڱڻ�ǰ���ô�ֱ�ڵ����������Ļǽ����ڸ�����С����һ���ڻ���ǰ��פ��ۿ�����ͼ��С���ۿ��ñڻ����ݽ���ʾ��ͼ����֪�ڻ��߶�AB��2�ף��ڻ��������ľ���BO��1�ף�����Ļǽ��ڻ�֮��ľ���OC��1�ף���С��������Ϊa�ף�0��a��3�������ڱڻ���ǰ��x�״��ۿ�����xΪ����ʱ��С���ۿ�����ڻ������������ɵ��ӽǦ����
���쳤���ڼ�С��ȥ�ιۻ�չ��Ϊ�˱����ڻ����ٰ췽�ڱڻ�ǰ���ô�ֱ�ڵ����������Ļǽ����ڸ�����С����һ���ڻ���ǰ��פ��ۿ�����ͼ��С���ۿ��ñڻ����ݽ���ʾ��ͼ����֪�ڻ��߶�AB��2�ף��ڻ��������ľ���BO��1�ף�����Ļǽ��ڻ�֮��ľ���OC��1�ף���С��������Ϊa�ף�0��a��3�������ڱڻ���ǰ��x�״��ۿ�����xΪ����ʱ��С���ۿ�����ڻ������������ɵ��ӽǦ����������ͨ��0��a��1��1��a��3��a��2���ֱ����tan�ȣ����캯��ͨ�������ĵ�����������������ֵ��˵���ӽ����
�������С������16�֣�
�⣺��Ϊy=tanx��x�ʣ�0��
������������
��1����0��a��1ʱ����ͼ1��tan��=tan����-�£�=
=
��
���f��x��=x+
����֤������f��x���ڣ�0��
���ǵ�����������
��(
��+��)�ǵ�����������
��
��1ʱ����2-
��a��1ʱ��
f��x����[1��+�ޣ���������������ʱ��x=1ʱtan��ȡ�����ֵ�����ӽǦ����
��
��1ʱ����0��a��2-
��
�ٵ�x=
ʱ��tan��ȡ�����ֵ�����ӽǦ����
�ڵ�a=1ʱ��tan��=
��x��1������x=1ʱtan��ȡ�����ֵ�����ӽǦ����
��2����1��a��3��a��2ʱ��ͼ2��
tan�ȨTtan����+�£�=
=
��
��g��x��=x-
��
��[1��+�ޣ����������������Ե�x=1ʱ��ymax��0��tan�ȣ�0���ʦ�Ϊ��ǣ�
�൱x=1ʱ��g��x��ȡ����Сֵ��tan��ȡ�����ֵ�����ӽǦ����
���ϣ���2-
��a��3ʱ����x=1ʱ���ӽǦ����
��0��a��2-
��ʱ����x=
ʱ���ӽǦ����
�⣺��Ϊy=tanx��x�ʣ�0��
| �� |
| 2 |
��1����0��a��1ʱ����ͼ1��tan��=tan����-�£�=
| ||||
1+
|
| 2 | ||
x+
|
���f��x��=x+
| (1-a)(3-a) |
| x |
| (1-a)(3-a) |
��(
| (1-a)(3a) |
��
| (1-a)(3-a) |
| 2 |
f��x����[1��+�ޣ���������������ʱ��x=1ʱtan��ȡ�����ֵ�����ӽǦ����
��
| (1-a)(3-a) |
| 2 |
�ٵ�x=
| (1-a)(3-a) |
�ڵ�a=1ʱ��tan��=
| 2 |
| x |
��2����1��a��3��a��2ʱ��ͼ2��
tan�ȨTtan����+�£�=
| ||||
1-
|
| 2 | ||
x-
|
��g��x��=x-
| (a-1)(3-a) |
| x |
��[1��+�ޣ����������������Ե�x=1ʱ��ymax��0��tan�ȣ�0���ʦ�Ϊ��ǣ�
�൱x=1ʱ��g��x��ȡ����Сֵ��tan��ȡ�����ֵ�����ӽǦ����
���ϣ���2-
| 2 |
��0��a��2-
| 2 |
| (1-a)(3-a) |
���������⿼��������ε�ʵ��Ӧ�ã����麯���ĵ����Ե�Ӧ�ã���������˼�룬����������

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
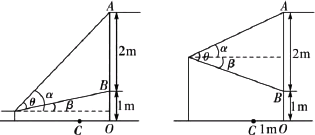
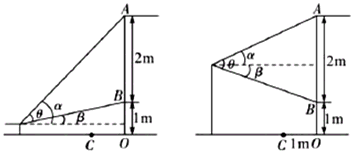 ���쳤���ڼ�С��ȥ�ιۻ�չ��Ϊ�˱����ڻ����ٰ췽�ڱڻ�ǰ���ô�ֱ�ڵ����������Ļǽ����ڸ�����С����һ���ڻ���ǰ��פ��ۿ�����ͼ��С���ۿ��ñڻ����ݽ���ʾ��ͼ����֪�ڻ��߶�AB��2�ף��ڻ��������ľ���BO��1�ף�����Ļǽ��ڻ�֮��ľ���OC��1�ף���С��������Ϊa�ף�0��a��3�������ڱڻ���ǰ��x�״��ۿ�����xΪ����ʱ��С���ۿ�����ڻ������������ɵ��ӽǦ����
���쳤���ڼ�С��ȥ�ιۻ�չ��Ϊ�˱����ڻ����ٰ췽�ڱڻ�ǰ���ô�ֱ�ڵ����������Ļǽ����ڸ�����С����һ���ڻ���ǰ��פ��ۿ�����ͼ��С���ۿ��ñڻ����ݽ���ʾ��ͼ����֪�ڻ��߶�AB��2�ף��ڻ��������ľ���BO��1�ף�����Ļǽ��ڻ�֮��ľ���OC��1�ף���С��������Ϊa�ף�0��a��3�������ڱڻ���ǰ��x�״��ۿ�����xΪ����ʱ��С���ۿ�����ڻ������������ɵ��ӽǦ����