题目内容
(本题满分12分)
已知二次函数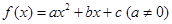 满足
满足 且
且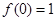 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)当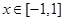 时,不等式:
时,不等式: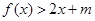 恒成立,求实数
恒成立,求实数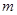 的范围.
的范围.
【答案】
(Ⅰ)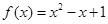 ;(Ⅱ)
;(Ⅱ)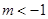
【解析】
试题分析:(Ⅰ)令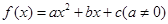 代入:
代入:
得: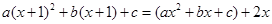
即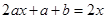 对于任意的
对于任意的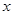 成立,则有
成立,则有
∴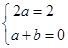 解得
解得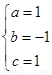 ∴
∴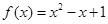 6分
6分
(Ⅱ)当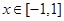 时,
时,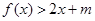 恒成立
恒成立
即: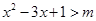 恒成立;
8分
恒成立;
8分
令 ,
,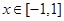
∵开口方向向上,对称轴: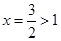 ,∴
,∴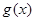 在
在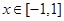 内单调递减;
内单调递减;
∴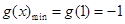 ∴
∴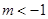 12分
12分
考点:本题考查了函数解析式的求法及恒成立问题
点评:二次函数在指定区间上的恒成立问题,可以利用韦达定理以及根的分布知识求解,属基础题

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面