题目内容
某地发生特大地震和海啸,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为m的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中f(x)=
|
(1)如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在7天(从投放药剂算起包括7天)之内的自来水达到最佳净化,试确定该投放的药剂质量m的值.
分析:(1)由m=4,且y=m•f(x),可得药剂在水中释放浓度y的函数;因为函数y是分段函数,在求释放浓度不低于4(即y≥4)时,要分区间去求解.
(2)由函数y是分段函数,故分区间讨论函数的单调性,从而求得y的取值范围,即药剂在水中释放浓度的大小;为使最佳净化,即4≤y≤10恒成立,只要使y的取值范围在区间[4,10]内即可,从而解出m的值.
(2)由函数y是分段函数,故分区间讨论函数的单调性,从而求得y的取值范围,即药剂在水中释放浓度的大小;为使最佳净化,即4≤y≤10恒成立,只要使y的取值范围在区间[4,10]内即可,从而解出m的值.
解答:解:(1)因为m=4,所以y=m•f(x)=
;
所以,当0<x≤4时,x+8≥4显然成立,当x>4时,
≥4,得4<x≤8;综上知,0<x≤8;
所以,自来水达到有效净化一共可持续8天.
(2)由y=m•f(x)=
知,在区间(0,4]上单调递增,即2m<y≤3m,在区间(4,7]上单调递减,即
≤y<3m,综上知,
≤y≤3m;为使4≤y≤10恒成立,只要
≥4,且3m≤10即可,即m=
;
所以,为了使在7天之内的自来水达到最佳净化,该投放的药剂量应为
.
|
所以,当0<x≤4时,x+8≥4显然成立,当x>4时,
| 24 |
| x-2 |
所以,自来水达到有效净化一共可持续8天.
(2)由y=m•f(x)=
|
| 6m |
| 5 |
| 6m |
| 5 |
| 6m |
| 5 |
| 10 |
| 3 |
所以,为了使在7天之内的自来水达到最佳净化,该投放的药剂量应为
| 10 |
| 3 |
点评:本题考查了分段函数模型的灵活应用;分段函数求最值时,要在每一个区间上求出最值,再通过比较,得出函数的最值.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
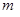 的药剂后,经过
的药剂后,经过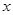 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度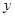 (毫克/升) 满足
(毫克/升) 满足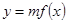 ,其中
,其中 ,当药剂在水中释放的浓度不低于
,当药剂在水中释放的浓度不低于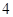 (毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于
(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于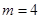 ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?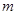 ,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量 ,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水口释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水口释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化. ,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水口释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水口释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化. ,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水口释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水口释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化.