题目内容
已知数列{an}中,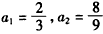 ,当n≥2时,3an+1=4an-an-1(n∈N*),
,当n≥2时,3an+1=4an-an-1(n∈N*),
(Ⅰ)证明:{an+1-an}为等比数列;
(Ⅱ)求数列{an}的通项;
(Ⅲ)若对任意n∈N*有λa1a2a3…an≥1(λ∈N*)均成立,求λ的最小值。
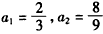 ,当n≥2时,3an+1=4an-an-1(n∈N*),
,当n≥2时,3an+1=4an-an-1(n∈N*),(Ⅰ)证明:{an+1-an}为等比数列;
(Ⅱ)求数列{an}的通项;
(Ⅲ)若对任意n∈N*有λa1a2a3…an≥1(λ∈N*)均成立,求λ的最小值。
(Ⅰ)证明:∵数列{an}中,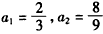 ,
,
当n≥2时,3an+1=4an-an-1(n∈N*),
∴当n≥2时,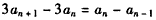 ,
,
即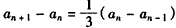 ,
,
所以,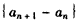 是以
是以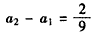 为首项,以
为首项,以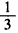 为公比的等比数列。
为公比的等比数列。
(Ⅱ)解:由(Ⅰ)知,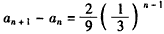 ,
,
故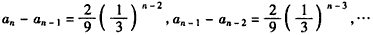
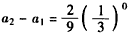 ,
,
累加,得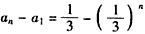 ,
,
所以,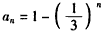 。
。
(Ⅲ)解:若对任意n∈N*有λa1a2a3…an≥1(λ∈N*)均成立,
即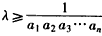 在n∈N*时恒成立,
在n∈N*时恒成立,
故需求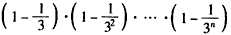 在n∈N*上的最小值,
在n∈N*上的最小值,
先证n∈N*时有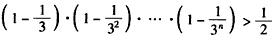 ,
,
显然,左边每个因式都是正数,先证明对每个n∈N*,有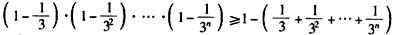 ,
,
用数学归纳法证明上式,
(ⅰ)n=1时,上式显然成立;
(ⅱ)假设n=k时,结论成立,
即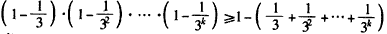 ,
,
则当n=k+1时,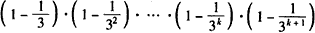
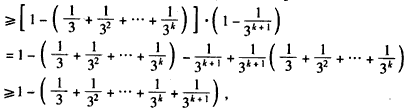
即当n=k+1时,结论也成立;
故对一切n∈N*,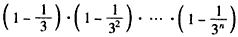
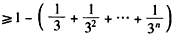 成立,
成立,
所以,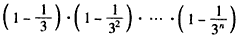
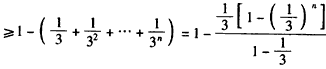
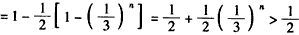 ,
,
∵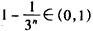 ,
,
易知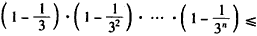
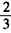 ,
,
故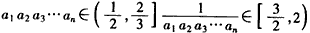 ,
,
而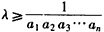 在n∈N*时恒成立且λ∈N*,
在n∈N*时恒成立且λ∈N*,
所以,λ的最小值为2。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|