题目内容
已知函数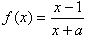 +ln(x+1),其中实数a≠-1。
+ln(x+1),其中实数a≠-1。
(1)若a=2,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在x=1处取得极值,试讨论f(x)的单调性。
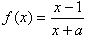 +ln(x+1),其中实数a≠-1。
+ln(x+1),其中实数a≠-1。(1)若a=2,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在x=1处取得极值,试讨论f(x)的单调性。
解:(1)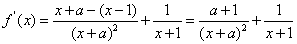
当a=2时,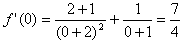
而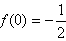
因此曲线y=f(x)在点(0,f(0))处的切线方程为y-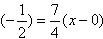
即7x-4y-2=0;
(2)因a≠-1,由(1)知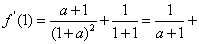
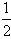
又因f(x)在x=1处取得极值,所以f'(1)=0
即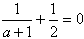
解得a=-3
此时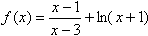 ,其定义域为(-1,3)∪(3,+∞)且
,其定义域为(-1,3)∪(3,+∞)且
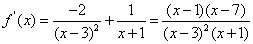
由f'(x)=0得x1=1,x2=7
当-1<x<1或x>7时,f'(x)>0
当1<x<7且x≠3时,f'(x)<0
由以上讨论知,f(x)在区间(-1,1],[7,+∞)上是增函数,在区间[1,3),(3,7]上是减函数。
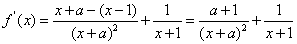
当a=2时,
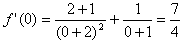
而
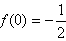
因此曲线y=f(x)在点(0,f(0))处的切线方程为y-
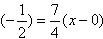
即7x-4y-2=0;
(2)因a≠-1,由(1)知
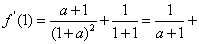
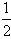
又因f(x)在x=1处取得极值,所以f'(1)=0
即
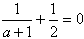
解得a=-3
此时
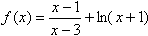 ,其定义域为(-1,3)∪(3,+∞)且
,其定义域为(-1,3)∪(3,+∞)且 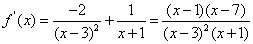
由f'(x)=0得x1=1,x2=7
当-1<x<1或x>
当1<x<7且x≠3时,f'(x)<0
由以上讨论知,f(x)在区间(-1,1],[7,+∞)上是增函数,在区间[1,3),(3,7]上是减函数。

练习册系列答案
相关题目