题目内容
过原点O的直线与函数y=2x的图象交于A,B两点,过B作y轴的垂线交函数y=4x的图象于点C,若AC平行于y轴,则点A的坐标是分析:先设A(n,2n),B(m,2m),则由过B作y轴的垂线交函数y=4x的图象于点C写出点C的坐标,再依据AC平行于y轴得出m,n之间的关系:n=
,最后根据A,B,O三点共线.利用斜率相等即可求得点A的坐标.
| m |
| 2 |
解答:解:设A(n,2n),B(m,2m),则
C(
,2m),
∵AC平行于y轴,
∴n=
,
∴A(
,2n),B(m,2m),
又A,B,O三点共线.
∴kOA=kOB
即
=
?n=m-1
又n=
,
n=1,
则点A的坐标是(1,2)
故答案为:(1,2).
C(
| m |
| 2 |
∵AC平行于y轴,
∴n=
| m |
| 2 |
∴A(
| m |
| 2 |
又A,B,O三点共线.
∴kOA=kOB
即
| 2n | ||
|
| 2m |
| m |
又n=
| m |
| 2 |
n=1,
则点A的坐标是(1,2)
故答案为:(1,2).
点评:本题主要考查了指数函数的图象与性质、直线的斜率公式、三点共线的判定方法等,属于基础题.

练习册系列答案
相关题目
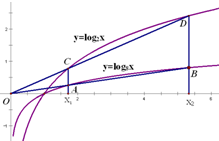 如图,已知过原点O的直线与函数y=log8x的图象交于A,B两点,分别过A,B作y轴的平行线与函数y=log2x的图象交于C,D两点;若BC∥x轴,则点A的坐标为
如图,已知过原点O的直线与函数y=log8x的图象交于A,B两点,分别过A,B作y轴的平行线与函数y=log2x的图象交于C,D两点;若BC∥x轴,则点A的坐标为 如图,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC恰好平行于y轴,则点A的坐标为
如图,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC恰好平行于y轴,则点A的坐标为 的图像交与A、B两点,
的图像交与A、B两点, 的图像于点C,若AC平行于y轴,
的图像于点C,若AC平行于y轴,
