题目内容
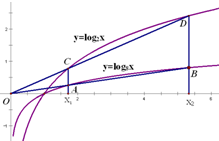 如图,已知过原点O的直线与函数y=log8x的图象交于A,B两点,分别过A,B作y轴的平行线与函数y=log2x的图象交于C,D两点;若BC∥x轴,则点A的坐标为
如图,已知过原点O的直线与函数y=log8x的图象交于A,B两点,分别过A,B作y轴的平行线与函数y=log2x的图象交于C,D两点;若BC∥x轴,则点A的坐标为(
,
log23)
| 3 |
| 1 |
| 6 |
(
,
log23)
.| 3 |
| 1 |
| 6 |
分析:设出A、B的坐标,解出C、D的坐标,根据OC、OD的斜率相等,利用三点共线得出A、B的坐标之间的关系.再根据BC平行x轴,B、C纵坐标相等,推出横坐标的关系,结合之前得出A、B的坐标之间的关系即可求出A的坐标.
解答:解:设点A、B的横坐标分别为x1、x2,
由题设知,x1>1,x2>1.则点A、B纵坐标分别为log8x1,log8x2,
因为A、B在过点O的直线上,所以
=
,
点C、D坐标分别为(x1,log2x1),(x2,log2x2).
由于BC平行于x轴,可知,
log2x1=log8x2,
即得log2x1=
log2x2,
∴x2=
.
代入x2log8x1=x1log8x2,得x12log8x1=3x1log8x1.
由于x1>1知log8x1≠0,
∴x12=3x1.
考虑x1>1,解得x1=
.
于是点A的坐标为(
,log8
),即A(
,
log23),
故答案为:(
,
log23).
由题设知,x1>1,x2>1.则点A、B纵坐标分别为log8x1,log8x2,
因为A、B在过点O的直线上,所以
| log8x1 |
| x1 |
| log8x2 |
| x2 |
点C、D坐标分别为(x1,log2x1),(x2,log2x2).
由于BC平行于x轴,可知,
log2x1=log8x2,
即得log2x1=
| 1 |
| 3 |
∴x2=
| x | 3 1 |
代入x2log8x1=x1log8x2,得x12log8x1=3x1log8x1.
由于x1>1知log8x1≠0,
∴x12=3x1.
考虑x1>1,解得x1=
| 3 |
于是点A的坐标为(
| 3 |
| 3 |
| 3 |
| 1 |
| 6 |
故答案为:(
| 3 |
| 1 |
| 6 |
点评:本小题主要考查对数函数图象、对数换底公式、对数方程、指数方程等基础知识,考查运算能力和分析问题的能力.属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
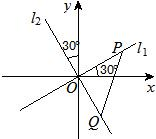 如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,已知线段PQ的长度为2,且点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动.
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,已知线段PQ的长度为2,且点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动.