Question

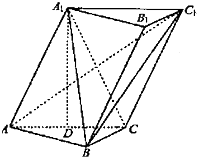（2013•太原一模）已知斜三棱柱ABC-A₁B₁C₁中，∠ACB=90°，AC=BC=2，点D为AC的中点，A₁D⊥平面ABC，A₁B⊥AC_l
（I）求证：AC₁⊥A_lC；
（Ⅱ）求三棱锥C_l-ABC的体积．

Answer 1

分析：（I）先由线线垂直证明线面垂直，再由线面垂直的性质证明线线垂直；
（II）先由线面垂直求棱锥的高，再根据三棱锥的体积公式计算即可

解答：解：（I）证明：∵A₁D⊥平面ABC，∴平面AA₁C₁C⊥平面ABC，
又∠ACB=90°，∴BC⊥AC，∴BC⊥平面AA₁C₁C，∴BC⊥AC₁，
∵A₁B⊥AC₁，∴AC₁⊥平面A₁BC，
∴AC₁⊥A₁C．
（II）∵AA₁C₁C是平行四边形，由（I）知AC₁⊥A₁C，
∴四边形AA₁C₁C是菱形，∴AA₁=AC=2，
∵A₁D⊥平面ABC，∴A₁D⊥AC，
∴点D为AC的中点，∴AD=1，A₁D=

3

，
∴VC1-ABC=VA1-ABC=

1

3

×

1

2

×AC×BC×A1D=

2 3

3

．
．

点评：本题考查线面垂直的性质及棱锥体积的计算．